Practical Geometry - Solutions 4
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 10 Practical Geometry (Ex. 10.4)
NCERT Solutions
Chapter 10 Practical Geometry (Ex. 10.4)
Question 1. Construct ABC, given A = B = and AB = 5.8 cm.
Answer: To construct: ABC where A = B = and AB = 5.8 cm.
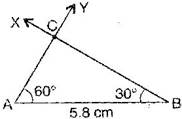
Steps of construction:

Steps of construction:
(a) Draw a line segment AB = 5.8 cm.
(b) At point A, draw an angle YAB = with the help of compass.
(c) At point B, draw XBA = with the help of compass.
(d) AY and BX intersect at the point C.
It is the required triangle ABC.
Question 2. Construct PQR if PQ = 5 cm, PQR = and QRP =
Answer: Given: PQR = and QRP =
We know that sum of angles of a triangle is
PQR + QRP + QPR =
QPR =
+ QPR =
QPR = –
QPR =
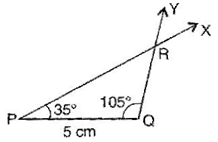
To construct: PQR where P = , Q = and PQ = 5 cm.

To construct: PQR where P = , Q = and PQ = 5 cm.
Steps of construction:
(a) Draw a line segment PQ = 5 cm.
(b) At point P, draw XPQ = with the help of protractor.
(c) At point Q, draw YQP = with the help of protractor.
(d) XP and YQ intersect at point R.
It is the required triangle PQR.
Question 3. Examine whether you can construct DEF such that EF = 7.2 cm, E = and F = Justify your answer.
Answer: Triangel DEF cannot be constructed since Angle E + Angle F = 110o + 80o = 190o
and the sum of all the angles of triangle is 180o.
