Practical Geometry-Solutions 14.6
CBSE Class –VI Mathematics
NCERT Solutions
Chaper 14 Practical Geometry (Ex. 14.6)
NCERT Solutions
Chaper 14 Practical Geometry (Ex. 14.6)
Question 1. Draw POA of measure and find its line of symmetry.
Answer: Steps of construction:
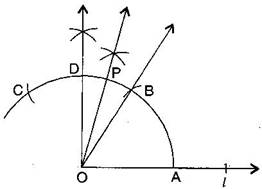
(a) Draw a line and mark a point O on it.
(b) Place the pointer of the compasses at O and draw an arc of any radius which intersects the line at A.
(c) Taking the same radius, with centre A, cut the previous arc at B.
(d) Join OB, then BOA =
(e) Taking the same radius, with centre B, cut the previous arc at C.
(f) Draw bisector of BOC. The angle is of Mark it at D. Thus, DOA =
(g) Draw as bisector of DOB.
Thus, POA =
Question 2. Draw an angle of measure and construct its bisector.
Answer: Steps of construction:

(a) Draw a ray
(b) With the help of protractor, construct AOB =
(c) Taking centre O and any convenient radius, draw an arc which intersects the arms and at P and Q respectively.
(d) Taking P as centre and radius more than half of PQ, draw an arc.
(e) Taking Q as the centre and with the same radius, draw another arc which intersects the previous at R.
(f) Join OR and produce it.
Thus, is the required bisector of AOB.
Question 3. Draw a right angle and construct its bisector.
Answer: Steps of construction:
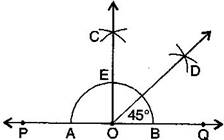
(a) Draw a line PQ and take a point O on it.
(b) Taking O as the centre and convenient radius, draw an arc which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d) Join OC. Thus, COQ is the required right angle.
(e) Taking B and E as centre and radius more than half of BE, draw two arcs which intersect each other at the point D.
(f) Join OD. Thus, is the required bisector of COQ.
Question 4. Draw an angle of measure and divide it into four equal parts.
Answer: Steps of construction:
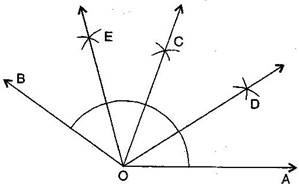
(a) Draw a ray
(b) At O, with the help of a protractor, construct AOB =
(c) Draw as the bisector of AOB.
(d) Again, draw as bisector of AOC.
(e) Again, draw as bisector of BOC.
(f) Thus, , and divide AOB in four equal arts.
Question 5. Construct with ruler and compasses, angles of following measures:
(a)
(b)
(c)
(d)
(e)
(f)
Answer:
Steps of construction:
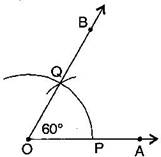
(a)
(i) Draw a ray
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects at P.
(iii) Taking P as the centre and the same radius, cut the previous arc at Q.
(iv) Join OQ and extend to B
Thus, BOA is required angle of
(b)
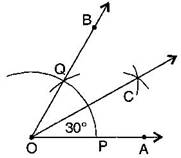
(i) Draw a ray
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects at P.
(iii) Taking P as the centre and the same radius, cut the previous arc at Q.
(iv) Join OQ. Thus, BOA is the required angle of
(v) Put the pointer on P and mark an arc.
(vi) Put the pointer on Q and with the same radius, cut the previous arc at C.
Thus, COA is required angle of
(c)
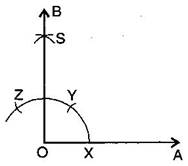
(i) Draw a ray
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects at X.
(iii) Taking X as the centre and the same radius, cut the previous arc at Y.
(iv) Taking Y as the centre and the same radius, draw another arc intersecting the same arc at Z.
(v) Taking Y and Z as centres and the same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to form a ray OB.
Thus, BOA is required angle of
(d)
(i) Draw a ray
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects at P.
(iii) Taking P as the centre and the same radius, cut the previous arc at Q.
(iv) Taking Q as the centre and the same radius cut the arc at S.
(v) Join OS.
Thus, AOD is required angle of
(e)
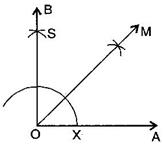 points y and z are not marked in the figure
points y and z are not marked in the figure(i) Draw a ray
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects at X.
(iii) Taking X as the centre and the same radius, cut the previous arc at Y.
(iv) Taking Y as the centre and the same radius, draw another arc intersecting the same arc at Z.
(v) Taking Y and Z as centres and the same radius, draw two arcs intersecting each other at S.
(vi) Join OS and produce it to form a ray OB. Thus, BOA is required angle of
(vii) Draw the bisector of BOA.
Thus, MOA is required angle of
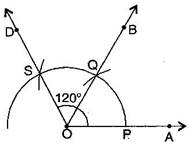
(f)
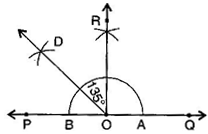
the angle 135 degrees should be shown in between QOD
(i) Draw a line PQ and take a point O on it.
(ii) Taking O as the centre and convenient radius, mark an arc, which intersects PQ at A and B.
(iii) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(iv) Join OR. Thus, QOR = POR =
(v) Draw the bisector of POR.
thus, QOD is the required angle of
Question 6.Draw an angle of measure and bisect it.
Answer: Steps of construction:
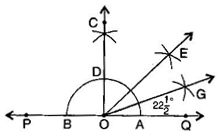
(a)Draw a line PQ and take a point O on it.
(b)Taking O as the centre and a convenient radius, draw an arc which intersects PQ at two points A and B.
(c)Taking A and B as centres and radius more than half of AB, draw two arcs which intersect each other at C.
(d)Join OC. Then COQ is an angle of
(e)Draw as the bisector of COQ. Thus, QOE =
(f)Again draw as the bisector of QOE.
Thus, QOG = EOG =
Question 7.Draw an angle of measure and bisect it.
Answer: Steps of construction:
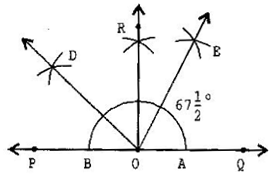
(a) Draw a line PQ and take a point O on it.
(b) Taking O as a centre and convenient radius, mark an arc, which intersects PQ at A and B.
(c) Taking A and B as centres and radius more than half of AB, draw two arcs intersecting each other at R.
(d) Join OR. Thus, QOR = POQ =
(e) Draw the bisector of POR. Thus, QOD is the required angle of
(f) Now, draw as the bisector of QOD.
Thus, QOE = DOE =
Question 8.Draw an angle of Make a copy of it using only a straight edge and compasses.
Answer: Steps of construction:
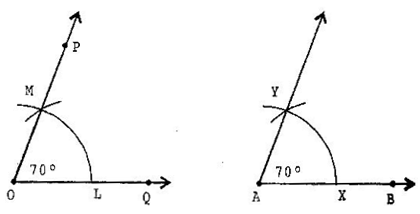
(a) Draw an angle with protractor, i.e.,

(a) Draw an angle with protractor, i.e.,
(b) Draw a ray
(c) Place the compasses at O and draw an arc to cut the rays of POQ at L and M.
(d) Use the same compasses, setting to draw an arc with A as the centre, cutting AB at X.
(e) Set your compasses setting to the length LM with the same radius.
(f) Place the compasses pointer at X and draw the arc to cut the arc drawn earlier at Y.
(g) Join AY.
Thus,
Question 9.Draw an angle of Copy its supplementary angle.
Answer: Steps of construction:
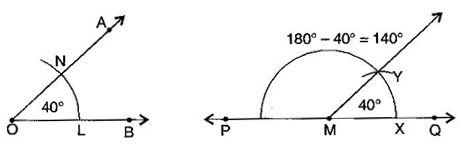

(a) Draw an angle of with the help of protractor, naming AOB.
(b) Draw a line PQ.
(c) Take any point M on PQ.
(d) Place the compasses at O and draw an arc to cut the rays of AOB at L and N.
(e) Use the same compasses setting to draw an arc M as centre, cutting MQ at X.
(f) Set your compasses to length LN with the same radius.
(g) Place the compasses at X and draw the arc to cut the arc drawn earlier Y.
(h) Join MY.
Thus, QMY = and PMY =100 degrees is supplementary of it.
