Practical Geometry-Solutions 14.4

CBSE Class –VI Mathematics
NCERT Solutions
Chaper 14 Practical Geometry (Ex. 14.4)

---

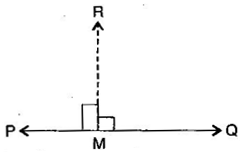
Question 1. Draw any line segment AB¯¯¯¯¯¯¯.$\overline{\text{AB}}.$ Mark any point M on it. Through M, draw a perpendicular to AB¯¯¯¯¯¯¯.$\overline{\text{AB}}.$ (Use ruler and compasses)

Answer: Steps of construction:

(i) With M as centre and a convenient radius, draw an arc intersecting the line AB at two points C and D.

(ii) With C and D as centres and a radius greater than MC, draw two arcs, which cut each other at P.

(iii) Join PM. Then PM is perpendicular to AB through the point M.

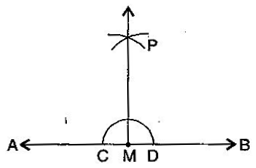
Question 2. Draw any line segment PQ¯¯¯¯¯¯¯.$\overline{\text{PQ}}.$ Take any point R not on it. Through R, draw a perpendicular to PQ¯¯¯¯¯¯¯.$\overline{\text{PQ}}.$ (Use ruler and set-square)

Answer: Steps of construction:

(i) Place a set-square on PQ¯¯¯¯¯¯¯$\overline{\text{PQ}}$ such that one arm of its right angle aligns along PQ¯¯¯¯¯¯¯$\overline{\text{PQ}}$.

(ii) Place a ruler along the edge opposite to the right angle of the set-square.

(iii) Hold the ruler fixed. Slide the set square along the ruler till the point R touches the other arm of the set square.

(iv) Join RM along the edge through R meeting PQ¯¯¯¯¯¯¯$\overline{\text{PQ}}$ at M. Then RM ⊥$\mathrm{\perp }$ PQ.

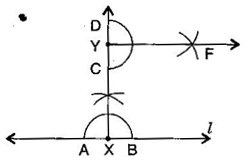
Question 3. Draw a line l$l$ and a point X on it. Through X, draw a line segment XY¯¯¯¯¯¯¯¯$\overline{\text{XY}}$ perpendicular to l.$l.$

Now draw a perpendicular to XY¯¯¯¯¯¯¯¯$\overline{\text{XY}}$ to Y. (use ruler and compasses)

Answer: Steps of construction:

(i) Draw a line ′l′${}^{\prime }{l}^{\prime }$ and take point X on it.

(ii) With X as centre and a convenient radius, draw an arc intersecting the line ′l′${}^{\prime }{l}^{\prime }$ at two points A and B.

(iii) With A and B as centres and a radius greater than XA, draw two arcs, which cut each other at C.

(iv) Join XC and produce it to Y. Then XY is perpendicular to ′l′${}^{\prime }{l}^{\prime }$.

(v) With Y as centre and a convenient radius, draw an arc intersecting XY at two points C and D.

(vi) With C and D as centres and radius greater than YD, draw two arcs which cut each other at F.

(vii) Join YF, then YF is perpendicular to XY at Y.