Practical Geometry-Solutions 14.2
CBSE Class –VI Mathematics
NCERT Solutions
Chapter 14 Practical Geometry (Ex. 14.2)
NCERT Solutions
Chapter 14 Practical Geometry (Ex. 14.2)
Question 1. Draw a line segment of length 7.3 cm, using a ruler.
Answer: Steps of construction:
(i) Place the zero mark of the ruler at a point A.
(ii) Mark a point B at a distance of 7.3 cm from A.
(iii) Join AB.
is the required line segment of length 7.3 cm.
(or)
(i) Place one of the pointers of the divider anywhere on the ruler say at 2 cm and count 7.3 cm and open the divider till there, in this case, it is 9.3cm. (It need not be started at 0 mark all the time).
(ii) remove the divider from the ruler and place it on the paper without disturbing and apply a small pressure so that the paper gets a prick from the needles of the divider.
(iii) Mark the pricks as points A and B
(iv) Join the points using a ruler.
Question 2. Construct a line segment of length 5.6 cm using ruler and compasses.
Answer: Steps of construction:
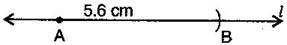
(i) Draw a line Mark a point A on this line.
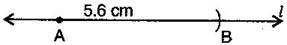
(i) Draw a line Mark a point A on this line.
(ii) Place the compasses pointer on zero mark of the ruler. Open it to place the pencil point up to 5.6 cm mark.
(iii) Without changing the opening of the compasses. Place the pointer on A and cut an arc at B.
is the required line segment of length 5.6 cm.
Question 3. Construct of length 7.8 cm. From this cut off of length 4.7 cm. Measure
Answer: Steps of construction:

(i) Place the zero mark of the ruler at A.

(i) Place the zero mark of the ruler at A.
(ii) Mark a point B at a distance 7.8 cm from A.
(iii) Again, mark a point C at a distance 4.7 from A.
By measuring , we find that BC = 3.1 cm
Question 4. Given of length 3.9 cm, construct such that the length is twice that of . Verify by measurement.

(Hint: Construct such that length of = length of ; then cut off such that also has the length of .

(Hint: Construct such that length of = length of ; then cut off such that also has the length of .
Answer: Steps of construction:
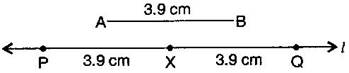
(i) Draw a line

(i) Draw a line
(ii) Construct such that length of = length of
(iii) Then cut of such that also has the length of
(iv) Thus the length of and the length of added together make twice the length of
Verification:
By measurement we find that PQ = 7.8 cm
= 3.9 cm + 3.9 cm = + = 2 x
Question 5. Given of length 7.3 cm and of length 3.4 cm, construct a line segment such that the length of is equal to the difference between the lengths of and Verify by measurement.
Answer: Steps of construction:
(i) Draw a line and take a point X on it.
(ii) Construct such that length = length of = 7.3 cm
(iii) Then cut off = length of = 3.4 cm
(iv) Thus the length of = length of – length of
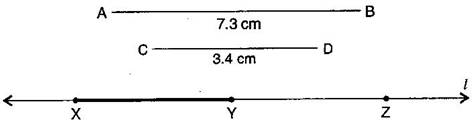
Verification:

Verification:
By measurement we find that length of = 3.9 cm = = 7.3 cm – 3.4 cm
