Perimeter and Area - Solutions 3

CBSE Class –VII Mathematics
NCERT Solutions
Chapter 11 Perimeter and Area (Ex. 11.3)

---

Question 1. Find the circumference of the circles with the following radius: (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

(a) 14 cm

(b) 28 mm

(c) 21 cm

Answer: (a) Circumference of the circle = 2πr$2\pi r$ = 2×227×14$2\times \frac{22}{7}\times 14$ = 88 cm

(b) Circumference of the circle = 2πr$2\pi r$ = 2×227×28$2\times \frac{22}{7}\times 28$ = 176 mm

(c) Circumference of the circle = 2πr$2\pi r$ = 2×227×21$2\times \frac{22}{7}\times 21$ = 132 cm

---

Question 2. Find the area of the following circles, given that: (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

(a) radius = 14 mm

(b) diameter = 49 m

(c) radius 5 cm

Answer: (a) Area of circle = πr2$\pi r^2$ = 227×14×14$\frac{22}{7}\times 14\times 14$ = 22 x 2 x 14 = 616 mm2

(b) Diameter = 49 m

∴$\therefore$ radius = 492$\frac{49}{2}$ = 24.5 m

∴$\therefore$ Area of circle = πr2$\pi r^2$ = 227×24.5×24.5$\frac{22}{7}\times 24.5\times 24.5$ = 22 x 3.5 x 24.5 = 1886.5 m2

(c) Area of circle = πr2$\pi r^2$ = 227×5×5$\frac{22}{7}\times 5\times 5$ =  5507$\frac{550}{7}$ cm2

---

Question 3. If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

Answer: Circumference of the circular sheet = 154 m

⇒$\Rightarrow$ 2πr$2\pi r$ = 154 m ⇒$\Rightarrow$ r=1542π$r=\frac{154}{2\pi }$

⇒$\Rightarrow$ r=154×72×22$r=\frac{154\times 7}{2\times 22}$ = 24.5 m

Now, Area of circular sheet = πr2$\pi r^2$ = 227×24.5×24.5$\frac{22}{7}\times 24.5\times 24.5$= 22 x 3.5 x 24.5 = 1886.5 m2

Thus, the radius and area of circular sheet are 24.5 m and 1886.5 m2 respectively.

---

Question 4. A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds of fence. Also, find the costs of the rope, if it cost Rs. 4 per meter. (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

Answer: Diameter of the circular garden = 21 m

∴$\therefore$ Radius of the circular garden = 212$\frac{21}{2}$ m

Now, Circumference of circular garden = 2πr$2\pi r$ = 2×227×212$2\times \frac{22}{7}\times \frac{21}{2}$ = 2 x 11 x 3 = 22 x 3 = 66 m

The gardener makes 2 rounds of fence so the total length of the rope of fencing

= 2 x 2πr$2\pi r$ = 2 x 66 = 132 m

Since the cost of 1 meter rope = Rs. 4

Therefore, cost of 132 meter rope = 4 x 132 = Rs. 528

---

Question 5. From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)$\left(\text{Take }\pi \text{ = 3}\text{.14}\right)$

Answer: Radius of circular sheet (R) = 4 cm and radius of removed circle (r) = 3 cm

Area of remaining sheet = Area of circular sheet – Area of removed circle

= πR2−πr2$\pi {\text{R}}^2-\pi r^2$ = π(R2−r2)$\pi \left({\text{R}}^2-r^2\right)$

= π(42−32)$\pi \left(4^2-3^2\right)$ = π(16−9)$\pi \left(16-9\right)$

= 3.14 x 7 = 21.98 cm2

Thus, the area of remaining sheet is 21.98 cm2.

---

Question 6. Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs Rs. 15. (Take π = 3.14)$\left(\text{Take }\pi \text{ = 3}\text{.14}\right)$

Answer: Diameter of the circular table cover = 1.5 m

∴$\therefore$ Radius of the circular table cover = 1.52$\frac{1.5}{2}$ m

Circumference of circular table cover = 2πr$2\pi r$ = 2×3.14×1.52$2\times 3.14\times \frac{1.5}{2}$ = 4.71 m

Therefore the length of required lace is 4.71 m.

Now the cost of 1 m lace = Rs. 15

Then the cost of 4.71 m lace = 15 x 4.71 = Rs. 70.65

Hence, the cost of 4.71 m lace is Rs. 70.65.

---

Question 7. Find the perimeter of the adjoining figure, which is a semicircle including its diameter.

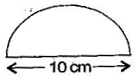
Answer: Diameter = 10 cm

∴$\therefore$ Radius = 102$\frac{10}{2}$ = 5 cm

According to question,

Perimeter of figure = Circumference of semi-circle + diameter

= πr$\pi r$ + D = 227×5+10$\frac{22}{7}\times 5+10$ = 1107+10$\frac{110}{7}+10$

= 110+707=1807$\frac{110+70}{7}=\frac{180}{7}$ = 25.71 cm

Thus, the perimeter of the given figure is 25.71 cm.

---

Question 8. Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is Rs. 15/m2. (Take π = 3.14)$\left(\text{Take }\pi \text{ = 3}\text{.14}\right)$

Answer: Diameter of the circular table top = 1.6 m

∴$\therefore$ Radius of the circular table top = 1.62=$\frac{1.6}{2}=$ 0.8 m

Area of circular table top = πr2$\pi r^2$ = 3.14 x 0.8 x 0.8 = 2.0096 m2

Now cost of 1 m2 polishing = Rs. 15

Then cost of 2.0096 m2 polishing = 15 x 2.0096 = Rs. 30.14 (approx.)

Thus, the cost of polishing a circular table top is Rs. 30.14 (approx.)

---

Question 9. Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

Answer: Total length of the wire = 44 cm

∴$\therefore$ the circumference of the circle = 2πr$2\pi r$ = 44 cm

⇒$\Rightarrow$ 2×227×r=44$2\times \frac{22}{7}\times r=44$ ⇒$\Rightarrow$ r=44×72×22$r=\frac{44\times 7}{2\times 22}$ = 7 cm

Now Area of the circle = πr2$\pi r^2$ = 227×7×7$\frac{22}{7}\times 7\times 7$ = 154 cm2

Now the wire is converted into square.

Then perimeter of square = 44 cm

⇒$\Rightarrow$ 4 x side = 44 ⇒$\Rightarrow$ side = 444$\frac{44}{4}$ = 11 cm

Now area of square = side x side = 11 x 11 = 121 cm2

Therefore, on comparing the area of circle is greater than that of square, so the circle enclosed more area.

---

Question 10. From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed (as shown in the adjoining figure). Find the area of the remaining sheet. (Take π = 227)$\left(\text{Take }\pi \text{ = }\frac{22}{7}\right)$

Answer: Radius of circular sheet (R) = 14 cm and Radius of smaller circle (r)$\left(r\right)$ = 3.5 cm

Length of rectangle (l)$\left(l\right)$ = 3 cm and breadth of rectangle (b)$\left(b\right)$ = 1 cm

According to question,

Area of remaining sheet = Area of circular sheet – (Area of two smaller circles + Area of rectangle)

= πR2−[2(πr2)+(l×b)]$\pi {\text{R}}^2-\left[2\left(\pi r^2\right)+\left(l\times b\right)\right]$

= 227×14×14−[(2×227×3.5×3.5)−(3×1)]$\frac{22}{7}\times 14\times 14-\left[\left(2\times \frac{22}{7}\times 3.5\times 3.5\right)-\left(3\times 1\right)\right]$

= 22 x 14 x 2 – [44 x 0.5 x 3.5 + 3]

= 616 – 80

= 536 cm2