Motion in A Straight Line - Test Papers

 CBSE Test Paper 01

Chapter 3 Motion in A Straight Line

---

1. For motion with uniform acceleration, x-t graph is 1

   1. a parabola
   2. a hyperbola
   3. a straight line
   4. a cubic

2. A jet lands on an aircraft carrier at 63 m/s. What is its acceleration in m/s2$\mathrm{m}/{\mathrm{s}}^2$ if it stops in 2.0 s? 1

   1. -35
   2. 34
   3. -31
   4. -33

3. A ball starts from rest and accelerates at 0.500 m/s2$\mathrm{m}/{\mathrm{s}}^2$ while moving down an inclined plane 9.00 m long. When it reaches the bottom, the ball rolls up another plane, where, after moving 15.0 m, it comes to rest. What is the speed of the ball in m/s at the bottom of the first plane? 1

   1. 3.0
   2. 1.00
   3. 2.00
   4. 4.00

4. A golf ball is released from rest from the top of a very tall building. Calculate the position in m of the ball after 2.00 s 1

   1. -32.1
   2. -19.6
   3. -22.2
   4. -20.9

5. A drag racer starts her car from rest and accelerates at 10.0 m/s2$\mathrm{m}/{\mathrm{s}}^2$ for the entire distance of 400 m .How long did it take the race car to travel this distance in s? 1

   1. 9.01
   2. 8.33
   3. 10.2
   4. 8.94

6. Can a body have zero velocity and still be accelerating? If yes, give any situation. 1

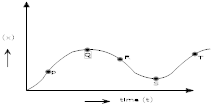
7. Figure shows a displacement- time graph. Comment on the sign of velocities at point P, Q, R, S and T. 1
   

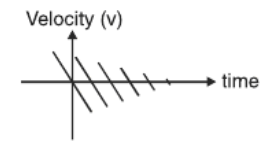
8. Suggest a suitable physical situation for the following graph. 1
   

9. A person travels along a straight road for the first half with a velocity v1 and the second half with velocity v2. What is the mean velocity of the person for the whole journey? 2

10. Write the characteristics of displacement. 2

11. Sameer went on his bike from Delhi to Gurgaon at a speed of 60km/hr and came back at a speed of 40km/hr. what is his average speed for entire journey. 2

12. A particle moving in a straight line covers half the distance with a speed of 3 m/s. The other half of distance is covered in two equal intervals of time with speeds of 4.5 m/s and 7.5 m/s, respectively. Find the average speed of the particle during this motion. 3

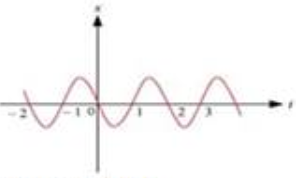
13. Figure gives the x-t plot of a particle executing one-dimensional simple harmonic motion. Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s, -1.2 s. 3
    

14. A particle is moving along a straight line and its position is given by the relation x = (t3 - 6t2 - 15t + 40)m 3
    Find

    1. The time at which velocity is zero.
    2. Position & Displacement at this point
    3. Acceleration for the particle at the point.

15. Two particles move along x - axis. The position of particle 1 is given by x = 6.00t2 + 3.00t + 2.00 (in metre and in seconds); acceleration of particle 2 is given by a = - 8.00 t(in m/s2 and seconds) and at t = 0, its velocity is 20 m/s. When the velocities of the particles match, find their velocities. 5

CBSE Test Paper 01
Chapter 3 Motion in A Straight Line

---

Answer

1. 1. a parabola
      Explanation: the slope of the x-t grpah will give you velocity. So, if u=0, the slope of graph at t=0 is 0.
      for u>0 case, the initial slope is +ve and for negative u, the initial slope is negative now, s = ut + 0.5at2, where acceleration=a let initial position is x​​​​​​o,
      x = x​xo + ut + 0.5at2,
      Hence you will get parabolic shapes.

2. 3. -31
      Explanation: Initial velocity u = 63 m/s
      As it stops, so final velocity v = 0 m/s
      Time t = 2.0 s
      We know
      v - u = at
      ⇒a=v−ut$\Rightarrow a=\frac{v-u}{t}$
      ⇒a=0−632$\Rightarrow a=\frac{0-63}{2}$
      ⇒a=−31.0 m/s2$\Rightarrow a=-31.0m/s^2$

3. 1. 3.0
      Explanation: For First Plane
      Initial velocity u = 0
      Acceleration a = 0.500 m/s​​​​​​2
      Distance covered s = 9.0 m
      Final velocity v = ?
      We know
      v2−u2=2as$v^2-u^2=2as$
      ⇒v2−0=2×0.500×9.0$\Rightarrow v^2-0=2\times 0.500\times 9.0$
      ⇒v2=9$\Rightarrow v^2=9$
      ⇒$\Rightarrow$ v = 3 m/s
      This is initial velocity for second plane

4. 2. -19.6
      Explanation: Ball is under free fall, acceleration ll be due to gravity
      Initial velocity u = 0
      Time = 2.0 seconds
      acceleration due to gravity g = - 9.8 ms-2
      We know
      S = ut + 12gt2$\frac{1}{2}g{t}^2$
      = 0×t+12×(−9.8)×(2.0)2$\times t+\frac{1}{2}\times (-9.8)\times (2.0{)}^2$
      = -19.6 m

5. 4. 8.94
      Explanation: Initial velocity u = 0
      Acceleration a = 10.0 m/s​​​​​​2
      Distance covered s = 400 m
      Time taken t = ?
      We know
      s=ut+12at2$s=ut+\frac{1}{2}a{t}^2$
      ⇒400=0×t+12×10×t2$\Rightarrow 400=0\times t+\frac{1}{2}\times 10\times t^2$
      ⇒400=5t2$\Rightarrow 400=5t^2$
      ⇒t2=80$\Rightarrow t^2=80$
      ⇒t=80−−√=8.94 s$\Rightarrow t=\sqrt{80}=8.94s$

6. Yes, at the highest point of vertical upward motion under gravity.

7. Velocity at P and T is positive
   Velocity at Q and S is zero
   Velocity at R is negative

8. A ball thrown up with some initial velocity rebounding from the floor with reduced speed after each hit.

9. Time to travel first half
   t1 = (d/2)v1$\frac{(d/2)}{v_1}$ = d2v1$\frac{d}{2v_1}$
   Time to travel second half
   t2 = d/2v2$\frac{d/2}{v_2}$ = d2v2$\frac{d}{2v_2}$
   ∴$\therefore$ Total time = t1 + t2 = d2[1v1+1v2]=d(v1+v2)2v1v2$\frac{d}{2}\left[\frac{1}{v_1}+\frac{1}{v_2}\right]=\frac{d(v_1+v_2)}{2v_1{v}_2}$
   ∴$\therefore$ Mean velocity or average velocity is given by
   = total distance / total time taken
   = dt1 + t2 = 2v1 + v2(v1 + v2)$\frac{\text{d}}{{\text{t}}_{\text{1}}\text{ + }{\text{t}}_{\text{2}}}\text{ = }\frac{\text{2}{\text{v}}_{\text{1}}\text{ + }{\text{v}}_{\text{2}}}{\text{(}{\text{v}}_{\text{1}}\text{ + }{\text{v}}_{\text{2}}\text{)}}$

10. 1. It is a vector quantity having both magnitude and direction.
    2. Displacement of a given body can be positive, negative or zero.

11. The average speed is given by
    Vav=2V1V2V1+V2$V_{av}=\frac{2V_1{V}_2}{V_1+V_2}$
    Vav=2×60×4060+40=4800100$V_{av}=\frac{2\times 60\times 40}{60+40}=\frac{4800}{100}$
    Vav = 48 km/hr

12. We know that Speed = distancetime$\frac{distance}{time}$
    Time to cover s2$\frac{s}{2}$ distance, t1 = s/23=s6s$\frac{s/2}{3}=\frac{s}{6}s$
    Time to cover s1 distance, t2 = s14.5s$\frac{s_1}{4.5}s$
    Time to cover s2 distance, t3 = s17.5s$\frac{s_1}{7.5}s$
    Now, s1 + s2 = s2$\frac{s}{2}$
    Therefore, 4.5t2+7.5t3=s2$4.5t_2+7.5t_3=\frac{s}{2}$
    Since, t2 = t3 ( given )
    ⇒4.5t2+7.5t2=s2⇒t2=s24s$\Rightarrow 4.5t_2+7.5t_2=\frac{s}{2}\Rightarrow t_2=\frac{s}{24}s$
    Total time = t1 + t2 + t3 = s6+s24+s24=624s=14s$\frac{s}{6}+\frac{s}{24}+\frac{s}{24}=\frac{6}{24}s=\frac{1}{4}s$
    Therefore, sav= ss/4$\frac{s}{s/4}$= 4 m/s.
    Hence average speed is 4 m/s

13. Negative, Negative, Positive (at t = 0.3 s)
    Positive, Positive, Negative (at t = 1.2 s)
    Negative, Positive, Positive (at t = -1.2 s)
    For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
    a = −ω2x$-{\omega }^{2}x$, ω→$\omega \to$ angular frequency, x→$x\to$ displacement…(i)
    and velocity of the particle, v = dxdt$\frac{dx}{dt}$, dxdt→$\frac{dx}{dt}\to$ slope of x-t plot.....(ii)
    Now at t = 0.3 s
    In this time interval, x is negative. Thus, the slope of the x-t plot will also be negative from equation (ii). Again, velocity is the slope of x-t plot. Therefore, both position and velocity are negative. However, using equation (i), acceleration of the particle will be positive.
    Now at t = 1.2 s
    In this time interval, x is positive. Thus, the slope of the x-t plot i.e. the velocity of the particle will also be positive from equation (ii).
    Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative.
    And at t = -1.2 s
    In this time interval, x is negative and t is also negative. Hence, the slope of the x-t plot i.e. the velocity of the particle will be positive here from equation (ii). From equation (i), it can be inferred that the acceleration of the particle will be positive, as x is negative.

14. x = t3 - 6t2 - 15t + 40
    υ=dxdt=(3t2−12t−15)m/s$\upsilon =\frac{dx}{dt}=\left(3t^2-12t-15\right)m/s$
    a=dvdt=(6t−12)m/s2$a=\frac{dv}{dt}=(6t-12)m/s^2$
    i) Since , v = 0
    3t2 - 12t - 15 = 0
    3t2 - 15t + 3t - 15 = 0
    3t(t - 5) + 3(t - 5) = 0
    (3t + 3)(t - 5) = 0
    Either t = -1 or t = 5
    Time cannot be negative
    ∴$\therefore$ t = 5 seconds.
    ii) Position at t = 5 s
    x = (5)3 - 6(5)2 - 15(5) + 40
    x = -60m
    At t = 0 s,
    x = ( 0 )3 - 6x( 0 )2 - 15x0 + 40 = 40 m
    Displacement between t = 0 sec to t = 5 sec
    S = Final Position ( x5 ) - Initial Position ( x0 )
    x5 = -60m
    x0 = 40m
    s = -60 - 40
    s = -100 m
    iii) Acceleration at t = 5s
    a = 6t - 12
    a = 6(5) - 12
    a = (30 - 12)
    a = 18m/s2

15. For particle 1, the position is given by:
    x1 = 6.00t2 + 3.00t + 2.00
    For particle 2,
    a2 = -8.00t,
    v2 = 20 m/s at t = 0 s
    We know that, v(t)=dxdt$v(t)=\frac{dx}{dt}$
    v(t) = 12t + 3 + 0
    v(t) = 12t + 3
    Also we can write ∫a(t)dt=v(t)$\int a(t)dt=v(t)$
    ⇒v(t)=∫−8.00dt$\Rightarrow v(t)=\int -8.00dt$ =−8∫tdt=−8t22+C$=-8\int tdt=\frac{-8t^2}{2}+C$
    v(t) = -4t2 + C
    If v(t) = 20 m/s and t = 0 s, then we have
    20 m/s = -4(0)2 + C
    ⇒20=0+C$\Rightarrow 20=0+C$
    ⇒C=20$\Rightarrow C=20$
    so, v2(t) = -4t2 + 20
    Since, velocities of two particles have to match, we need to set the two equations equal to each other, that is,
    v1(t) = v2(t)
    12t + 3 = -4t2 + 20
    4t2 + 12t - 17 = 0
    t=−12±(12)2−4(4)(−17)√2(4)$t=\frac{-12\pm \sqrt{(12{)}^2-4(4)(-17)}}{2(4)}$
    =−12±144+272√8$=\frac{-12\pm \sqrt{144+272}}{8}$
    t=−12±416√8=−12±20.38$t=\frac{-12\pm \sqrt{416}}{8}=\frac{-12\pm 20.3}{8}$
    t = - 4.04 s or t = 1.4 s
    therefore, t = 1.04 s ( reject t = - 4.04)
    Now, find the velocities of different particles,
    v(t1) = 12(1.04) + 3 = 15.48 m/s
    v(t2) = -4(1.04)2 + 20 = 15.67 m/s