Motion in A Straight Line - Revision Notes
CBSE Class XI PHYSICS
- Position, path length and displacement
- Velocity and Speed
- Acceleration and Relative velocity
- Kinematic equations for uniformly accelerated motion
1. An object is said to be in motion if its position changes with time. The position of the object can be specified with reference to a conveniently chosen origin. For motion in a straight line, position to the right of the origin is taken as positive and to the left as negative.
2. Path length is defined as the total length of the path traversed by an object.
3. Displacement is the change in position: . Path length is greater or equal to the magnitude of the displacement between the two points.
4. An object is said to be in uniform motion in a straight line if its displacement is equal in equal intervals of time. Otherwise, the motion is said to be non-uniform.
5. Average velocity is the displacement divided by the time interval in which the displacement occurs: . It is a vector quantity and its SI unit is m/s.
On an x-t graph, the average velocity over a time interval is the slope of the line connecting the initial and final positions corresponding to that interval.
6. Average Speed is the ratio of total path length traversed and the corresponding time interval. It is a scalar quantity and its SI unit is same (m/s) as that of velocity.
The average speed of an object may be greater or equal to the magnitude of the average velocity over a given time interval.
7. Instantaneous velocity or simply velocity is defined as the limit of the average velocity as the time interval Δt becomes infinitesimally small: . It is also a vector quantity and its SI unit is m/s.
The velocity at a particular instant is equal to the slope of the tangent drawn onposition-time graph at that instant.
8. Average acceleration is the change in velocity divided by the time interval during which the change occurs:
It is a scalar quantity and its SI unit is m/s2.
9. Instantaneous acceleration is defined as the limit of the average acceleration as the time interval Δt goes to zero:
It is a vector quantity and its SI unit is m/s2.
The acceleration of an object at a particular time is the slope of the velocity-time graph at that instant of time. For uniform motion, acceleration is zero and the x-t graph is a straight line inclined to the time axis and the v-t graph is a straight line parallel to the time axis. For motion with uniform acceleration, x-t graph is a parabola while the v-t graph is a straight line inclined to the time axis.
10. The area under the velocity-time curve between times and is equal to the displacement of the object during that interval of time.
11. For objects in uniformly accelerated rectilinear motion, the five quantities, displacement x, time taken t, initial velocity v0, final velocity v and acceleration a are related by a setof simple equations called kinematic equations of motion :
provided the position of the object at time t = 0 is 0.
If the particle starts at x = x0 , x in above equations is replaced by (x-).
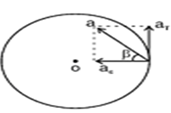
- When a body moves in a circular path with Increasing angular velocity, it has two linear accelerations.
(i) Centripetal acceleration ac and tangential acceleration aT. Resultant acceleration of the body is at an angle Beta given by
Where Beta is the angle between a and .
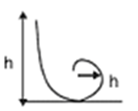
- The minimum height through which a motor cyclist has to descend to a vertical loop of radius r is h=
- Circular Motion
- Angular displacement : The angular displacement of an object moving around a circular path is defined as the angle subtended by the radius vector at the centre of the circular path in the given time.
- Angular velocity: It is defined as the time rate of change of angular displacement of the object =. Its S.I unit is rad/s.
- Uniform circular motion: when a point object is moving on a circular path with a constant speed ,then the motion of the object is said to be a uniform circular motion.
- Centripetal acceleration: It is defined as the acceleration of an object undergoing uniform circular motion .It always acts along the radius towards the centre of the circular path. The magnitude of centripetal acceleration is, a = v2/r.
- The rate of change of angular velocity is called its angular acceleration.
- The acceleration which changes the magnitude of the velocity is called tangential acceleration. It is given by ,where is the angular acceleration,
The direction of tangential acceleration is along the tangent to curved path.
- velocity of projection at lowest point
- velocity at the highest point H is
- Tension at lowest point
- For oscillation in vertical circle
- For leaving the vertical circle somewhere between
- Acceleration of a body down a rough inclined plane a =
- When a person of mass m climbs up a rope with acceleration a, the tension in the rope is t = m(g+a)
When the person climbs down the rope with acceleration a, tension in the rope is T= m(g-a)
- Suppose two masses and are suspended vertically from a rigid support with the help of strings as shown in Fig. When mass is pulled down with a force F, then and
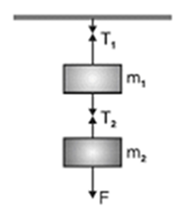
- When the same system of two masses attached to a string passes over a frictionless pulley at the edge of an inclined plane ,as shown in Fig.
Equation wil be…
- During motion on level curved road, the necessary centripetal force is provided by the force of friction between the tyres and the road. The maximum velocity with which a vehicle can go round a level curve without Skidding is
- To increase speed on turn, curved roads are usually baked outer edge of the curved road is raised suitably above the inner edge. If 0 (theta) is the angle of banking ,then .
When frictional force is ignored ,the optimum speed is
- While rounding a banked curved road ,maximum permissible speed is given by when friction is taken into account.
- When a cyclist takes a turn he bends a little inwards from his vertical position, while turning. Angle of bending from vertical position is given by
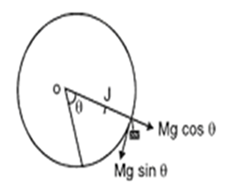
- Motion along a vertical circle is a non uniform circular motion. Tension in the string at any position is where is the angle of string with vertical line for looping with optimum speed:- (when tension at highest point is zero)
Impulse =
- Any system is said to be in equilibrium if net force applied on the system is zero . In this case system is either at rest or in uniform motion .
- Friction is the opposing force that comes into play when one body is actually moving over the surface of another body or one body is trying to move over the surface of the other,
Two causes of friction are: roughness of surface in contact;(ancient view) and,
Force of adhesion between the molecules of the surfaces in contact.(Modern view)
- Type of solid friction:-
- Static friction. It comes into effect when object is at rest but external force is applied.
- Dynamic friction .it comes into effect when object is in motion.
- Rolling friction-it comes into effect when object is rolling.
- Limiting friction is the maximum value of static friction, whereas dynamic/ Kinetic friction is somewhat less than the force of limiting friction.
- Coefficient of friction
When F= external force and R= normal reaction
- Angle of friction is the angle which resultant of F and R makes with the direction of R. The relation between
- Angle of repose(a) is the minimum angle of inclination of a plane with the horizontal ,such that a body placed on the plane just begins to slide down.
- Centripetal force is the force required to move a body uniformally in a circle.
