Motion in A Plane - Test Papers

 CBSE Test Paper 01

Chapter 4 Motion in A Plane

---

1. The speed of a projectile when it is at its greatest height is 25−−√$\sqrt{\frac{2}{5}}$ times its speed at half the max height. What is the angle of projection? 1
   1. 60o
   2. 90o
   3. 15o
   4. 45o
2. if particles A and B are moving with velocities vA${\mathbf{v}}_{\mathbf{A}}$ and vB${\mathbf{v}}_{\mathbf{B}}$ (each with respect to some common frame of reference, say ground.). Then, velocity of particle A relative to that of B is: 1
   1. vAB${\mathbf{v}}_{\mathbf{A}\mathbf{B}}$ = vA${\mathbf{v}}_{\mathbf{A}}$ + vB${\mathbf{v}}_{\mathbf{B}}$
   2. vAB${\mathbf{v}}_{\mathbf{A}\mathbf{B}}$ = vA${\mathbf{v}}_{\mathbf{A}}$ - vB${\mathbf{v}}_{\mathbf{B}}$
   3. vAB${\mathbf{v}}_{\mathbf{A}\mathbf{B}}$ = - vA${\mathbf{v}}_{\mathbf{A}}$ + vB${\mathbf{v}}_{\mathbf{B}}$
   4. vAB${\mathbf{v}}_{\mathbf{A}\mathbf{B}}$ = - vA${\mathbf{v}}_{\mathbf{A}}$ - vB${\mathbf{v}}_{\mathbf{B}}$
3. An airplane’s compass indicates that it is headed due north, and its airspeed indicator shows that it is moving through the air at 240 km/h. If there is a 100-km h wind from west to east. In what direction should the pilot head to travel due north? What will be her velocity relative to the earth? 1
   1. 35o W of N, 198 km/h
   2. 28o W of N, 210 km/h
   3. 25o W of N, 218 km/h
   4. 29o W of N, 200 km/h
4. The path of a projectile is 1
   1. cubic
   2. straight line
   3. hyperbola
   4. a parabola
5. Which of the following algebraic operations on vectors not permissible? 1
   1. adding a scalar component of the vector to the same vector
   2. multiplying any vector by any scalar,
   3. adding any two vectors
   4. multiplying the sum of vectors A and B by a scalar

6. What will be the net effect on maximum height of a projectile when its angle of projection is changed from 30° to 60°, keeping the same initial velocity of projection? 1

7. If |A×B|=A⋅B$|\mathbf{A}\times \mathbf{B}|=\mathbf{A}\cdot \mathbf{B}$, what is the angle between A and B? 1

8. Three vectors not lying in a plane can never end up to give a null vector. Justify. 1

9. A man can swim with a speed of 4 km/h in still water. How long does he take to cross a river 1 km wide, if the river flows steadily, 3 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank? 2

10. On a certain day, rain was falling vertically with a speed of 35 m/s. A wind started blowing after sometime with a speed of 12 m/s in East to West direction. In which direction should a boy waiting at a bus stop hold his umbrella? 2

11. What is the angle of projection at which horizontal range and maximum height are equal? 2

12. A boy stands at 78.4 m from a building and throws a ball which just enters a window 39.2 m above the ground. Calculate the velocity of projection of the ball. 3

13. Find the angle between the vectors A = i^−2j^−k^$\hat{\mathbf{i}}-2\hat{\mathbf{j}}-\hat{\mathbf{k}}$ and B = −i^+j^−2k^$-\hat{\mathbf{i}}+\hat{\mathbf{j}}-2\hat{\mathbf{k}}$. 3

14. An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s apart is 30°, what is the speed of the aircraft? 3

15. On an open ground, a motorist follows a track that turns to his left by an angle of 60o after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case. 5

CBSE Test Paper 01
Chapter 4 Motion in A Plane

---

Answer

1. 1. 60o
      Explanation: Time taken to reach the maximum height =usinθg$=\frac{usin\theta }{g}$
      Maximum height =u2sin2θ2g$=\frac{u^{2}si{n}^2\theta }{2g}$
      Half the maximum height =u2sin2θ4g$=\frac{u^{2}si{n}^2\theta }{4g}$
      Horizontal velocity at half the maximum height = ucosθ$ucos\theta$
      Vertical velocity at half the maximum height = usinθ2√$\frac{usin\theta }{\sqrt{2}}$
      Velocity at half the maximum height = u2cos2θ+u2sin2θ2−−−−−−−−−−−−−√$\sqrt{u^{2}co{s}^2\theta +\frac{u^{2}si{n}^2\theta }{2}}$
      According to question,
      ucosθ=25−−√u2cos2θ+u2sin2θ2−−−−−−−−−−−−−√$ucos\theta =\sqrt{\frac{2}{5}}\sqrt{u^{2}co{s}^2\theta +\frac{u^{2}si{n}^2\theta }{2}}$
      Squaring both sides,
      u2cos2θ=25u2(cos2θ+sin2θ2)$u^{2}co{s}^2\theta =\frac{2}{5}{u}^2(co{s}^2\theta +\frac{si{n}^2\theta }{2})$
      ⇒5−5sin2θ=2(1−sin2θ+sin2θ2)$\Rightarrow 5-5si{n}^2\theta =2(1-si{n}^2\theta +\frac{si{n}^2\theta }{2})$
      ⇒5−5sin2θ=2−sin2θ$\Rightarrow 5-5si{n}^2\theta =2-si{n}^2\theta$
      ⇒4sin2θ=3$\Rightarrow 4si{n}^2\theta =3$
      ⇒sinθ=3√2$\Rightarrow sin\theta =\frac{\sqrt{3}}{2}$
      ⇒θ=60o$\Rightarrow \theta ={60}^o$
2. 2. vAB${\mathbf{v}}_{\mathbf{A}\mathbf{B}}$ = vA${\mathbf{v}}_{\mathbf{A}}$ - vB${\mathbf{v}}_{\mathbf{B}}$
      Explanation: The relative velocity of an object A with respect to another object B is the velocity that object A would appear to have to an observer situated on object B moving along with it.
      In simple words relative velocity of A with respect to Be is the vector difference between the velocities of A and B.
      It is represented as
      VAB=VA−VB$V_{AB}=V_A-V_B$
3. 3. 25o W of N, 218 km/h
      Explanation: This is a relative velocity problem with vectors. Image given is a scale drawing of the situation. Again the vectors form a right triangle: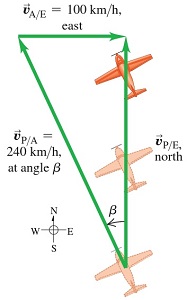
      
      v⃗ P/E=v⃗ P/A+v⃗ A/E${\overrightarrow{v}}_{P/E}={\overrightarrow{v}}_{P/A}+{\overrightarrow{v}}_{A/E}$
      As shown in image, The pilot points the nose of the airplane at an angle β$\beta$ into the wind to compensate for the crosswind. This angle, which tells us the direction of the vector v⃗ P/A${\overrightarrow{v}}_{P/A}$(the velocity of the airplane relative to the air), is one of our target variables. The other target variable is the speed of the airplane over the ground, which is the magnitude of the vector v⃗ P/E${\overrightarrow{v}}_{P/E}$ (the velocity of the airplane relative to the earth). The known and unknown quantities are:v⃗ P/E=${\overrightarrow{v}}_{P/E}=$ magnitude unknown due North
      v⃗ P/A${\overrightarrow{v}}_{P/A}$ = 240 km/h due north
      v⃗ A/E${\overrightarrow{v}}_{A/E}$ = 100 km/h due east
      We’ll solve for the target variables by using iimage and trigonometry.
      vP/E=(240)2−(100)2−−−−−−−−−−−−√$v_{P/E}=\sqrt{(240{)}^2-(100{)}^2}$=218km/h
      β=sin−1(100240)$\beta =si{n}^{-1}(\frac{100}{240})$= 25°
      The pilot should point the airplane 25° west of north, and her ground speed is then 218 km/h.
4. 4. a parabola
      Explanation: A particle with a vertical and horizontal velocity travelling in a gravitational field will trace out a parabola.
5. 1. adding a scalar component of the vector to the same vector
      Explanation: Although vectors and scalars represent different types of physical quantities, it is sometimes necessary for them to interact. While adding a scalar to a vector is impossible because of their different dimensions in space, it is possible to multiply a vector by a scalar.

6. Maximum height H of a projectile is given by the equation H = v02sin2θ/2g
   here, H∝sin2θ$H\propto {\sin }^2\theta$
   H1H2=(sin30∘)2(sin60∘)2=14×43=13$\frac{H_1}{H_2}=\frac{{\left(\sin {30}^{\circ }\right)}^2}{{\left(\sin {60}^{\circ }\right)}^2}=\frac{1}{4}\times \frac{4}{3}=\frac{1}{3}$
   or H2 = 3H1
   The maximum height of the projectile for angle of projection 60° is three times more than the maximum height at angle of projection 30°

7. As we know, A×B$\mathbf{A}\times \mathbf{B}$ = AB sinθ$\theta$
   and A.B = AB cos θ$\theta$
   It is given that the cross product of A and B is equal to its dot product, hence
   AB sinθ$\theta$ = AB cosθ$\theta$
   ⇒sinθcosθ=1$\Rightarrow \frac{\sin \theta }{\cos \theta }=1$
   ⇒tanθ=1$\Rightarrow \tan \theta =1$
   ⇒θ=45∘$\Rightarrow \theta ={45}^{\circ }$

8. As given three vectors are non coplanar vectors, therefore they cannot be represented by the three sides of a triangle taken in the same order. Hence in no possible way it can gives a sum of zero, i.e. null vector.

9. Given, speed of man(vm) = 4 km/h
   Speed of river(vr) = 3 km/h
   Width of the river(d) = 1 km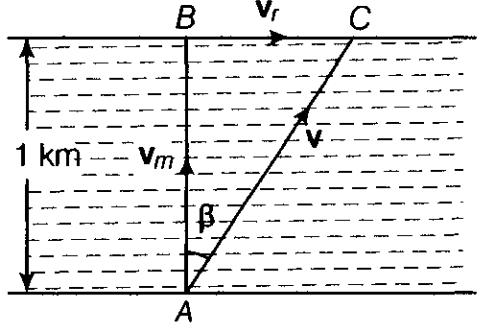
   
   Time taken by the man to cross the river,
   t =  Width of the river  Speed of the man =1km4km/h=14h=14×60$\frac{\text{ Width of the river }}{\text{ Speed of the man }}=\frac{1\mathrm{k}\mathrm{m}}{4\mathrm{k}\mathrm{m}/\mathrm{h}}=\frac{1}{4}\mathrm{h}=\frac{1}{4}\times 60$
   = 15 min
   Distance travelled along the river = vrt
   =3×14=34km=30004$=3\times \frac{1}{4}=\frac{3}{4}\mathrm{k}\mathrm{m}=\frac{3000}{4}$= 750 m

10. As shown in the figure the velocity of rain, VR = OA = 35 m/s, and the velocity of wind, Vw = OB =12 m/s. Here, OC represents the direction of resultant in which the boy should hold his umbrella,
    
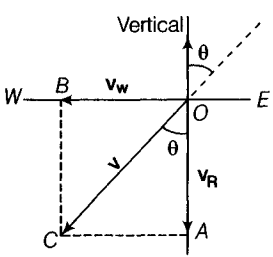
    Hence, the magnitude of the resultant velocity is
    v=(vR)2+(vW)2−−−−−−−−−−−√=(35)2+(12)2−−−−−−−−−−√$v=\sqrt{{\left(v_R\right)}^2+{\left(v_W\right)}^2}=\sqrt{(35{)}^2+(12{)}^2}$= 37 m/s
    Let the resultant velocity, v (=OC) make an angle θ$\theta$ with the vertical. Then,
    tanθ=ACOA=vWvR=1235=0.343$\tan \theta =\frac{AC}{OA}=\frac{v_W}{v_R}=\frac{12}{35}=0.343$
    ∴θ=tan−1(0.343)≃19∘$\therefore \theta ={\tan }^{-1}(0.343)\simeq {19}^{\circ }$ with respect to the direction of rainfall.

11. Equating,
    μ2sin2θg=u2sin2θ2g$\frac{{\mu }^2\sin 2\theta }{g}=\frac{u^2{\sin }^2\theta }{2g}$
    ∵u2sin2θg=R$\because \frac{u^2\sin 2\theta }{g}=R$(Horizontal Range)
    sin2θ=1/2sin2θ$\sin 2\theta =1/2{\sin }^2\theta$
    ∵u2sin2θ2g=hm$\because \frac{u^2{\sin }^2\theta }{2g}=h_m$ (Maximum Height)
    2sinθcosθ=1/2sin2θ$2\sin \theta \cos \theta =1/2{\sin }^2\theta$
    tanθ=4⇒θ=75.96∘$\tan \theta =4\Rightarrow \theta ={75.96}^{\circ }$

12. Consider a boy standing at position P at a horizontal distance 78.4m from the window, he throws a ball with a velocity u at an angle θ$\theta$ with the horizontal which just enters window W at a height 39.2 m.
    
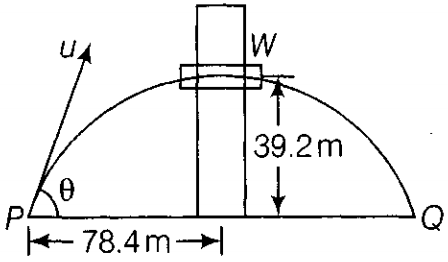
    For the maximum Height of projectile we have the relation, H = u2sin2θ2g⇒39.2m=u2sin2θ2g$\frac{u^2{\sin }^2\theta }{2g}\Rightarrow 39.2m=\frac{u^2{\sin }^2\theta }{2g}$........(i)
    and horizontal range, R=u2sin2θg$R=\frac{u^2\sin 2\theta }{g}$
    ⇒$\Rightarrow$2×78.4=u2sin2θg$2\times 78.4=\frac{u^2\sin 2\theta }{g}$...........(ii)
    Dividing Equations (i) and (ii), we get
    u2sin2θ2g×gu22sinθcosθ=39.22×78.4$\frac{u^2{\sin }^2\theta }{2g}\times \frac{g}{u^{2}2\sin \theta \cos \theta }=\frac{39.2}{2\times 78.4}$
    ⇒14tanθ=14⇒θ=45∘$\Rightarrow \frac{1}{4}\tan \theta =\frac{1}{4}\Rightarrow \theta ={45}^{\circ }$
    Substituting θ$\theta$ = 45° in Eq. (ii), we get
    u2sin90∘9.8=2×78.4$\frac{u^2\sin {90}^{\circ }}{9.8}=2\times 78.4$
    ⇒u=2×78.4×9.8−−−−−−−−−−−√$\Rightarrow u=\sqrt{2\times 78.4\times 9.8}$= 39.2 m/s
    Hence, the ball should be projected at an angle 45° with an initial speed of 39.2 m/s.

13. Given two vectors A = i^−2j^−k^$\hat{\mathbf{i}}-2\hat{\mathbf{j}}-\hat{\mathbf{k}}$ and B = −i^+j^−2k^$-\hat{\mathbf{i}}+\hat{\mathbf{j}}-2\hat{\mathbf{k}}$
    From the expression of dot product or scalar product.
    A.B = AB cos θ..........(i)
    The magnitude of A⃗ $\overrightarrow{A}$ is given by
    A=(1)2+(−2)2+(−1)2−−−−−−−−−−−−−−−−−√=6–√$A=\sqrt{(1{)}^2+(-2{)}^2+(-1{)}^2}=\sqrt{6}$..........(ii)
    The magnitude of B⃗ $\overrightarrow{B}$ is given by
    B=(−1)2+(1)2+(−2)2−−−−−−−−−−−−−−−−−√=6–√$B=\sqrt{(-1{)}^2+(1{)}^2+(-2{)}^2}=\sqrt{6}$........(iii)
    Now solving LHS of Eq (i)
    A.B = (i^−2j^−k^)⋅(−i^+j^−2k^)$(\hat{\mathbf{i}}-2\hat{\mathbf{j}}-\hat{\mathbf{k}})\cdot (-\hat{\mathbf{i}}+\hat{\mathbf{j}}-2\hat{\mathbf{k}})$
    =(1.−1)(i^⋅i^)+(1⋅1)(i^⋅j^)+(1⋅−2)(i^⋅k^)+(2⋅−1)$=(1.-1)(\hat{\mathbf{i}}\cdot \hat{\mathbf{i}})+(1\cdot 1)(\hat{\mathbf{i}}\cdot \hat{j})+(1\cdot -2)(\hat{\mathbf{i}}\cdot \hat{\mathbf{k}})+(2\cdot -1)$ (j^⋅i^)+(−2⋅1)(j^⋅j^)+(2⋅−2)(j^⋅k^)+(−1⋅−1)$(\hat{j}\cdot \hat{\mathbf{i}})+(-2\cdot 1)(\hat{\mathbf{j}}\cdot \hat{\mathbf{j}})+(2\cdot -2)(\hat{\mathbf{j}}\cdot \hat{\mathbf{k}})+(-1\cdot -1)$
    (k^⋅i^)+(−1⋅1)(k^⋅j^)+(−1⋅−2)(k^⋅k^)$(\hat{\mathbf{k}}\cdot \hat{\mathbf{i}})+(-1\cdot \mathbf{1})(\hat{\mathbf{k}}\cdot \hat{\mathbf{j}})+(-1\cdot -2)(\hat{\mathbf{k}}\cdot \hat{\mathbf{k}})$
    A.B = -1
    Substituting the values of A from Eq. (ii) and B from Eq. (iii) and A.B = -1 in Eq. (i), we get
    −1=(6–√)(6–√)cosθ$-1=(\sqrt{6})(\sqrt{6})\cos \theta$
    ⇒cosθ=−16⇒θ=cos−1(−16)=80.44∘$\Rightarrow \cos \theta =\frac{-1}{6}\Rightarrow \theta ={\cos }^{-1}\left(\frac{-1}{6}\right)={80.44}^{\circ }$in the third quadrant

14. The positions of the observer and the aircraft are shown in the given figure. The aircraft is following path PRQ and observer is at 'O'.
    
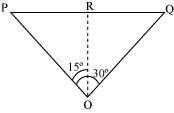
    Height of the aircraft from ground, OR = 3400 m
    Angle subtended between the position, ∠POQ=30∘$\mathrm{\angle }POQ={30}^{\circ }$
    Time interval, t = 10 s
    In ΔPRO$\mathrm{\Delta }PRO$
    tan15∘=PROR$\tan {15}^{\circ }=\frac{PR}{OR}$
    PR = OR tan 15o
    PR=3400×tan15∘$PR=3400\times \tan {15}^{\circ }$
    ΔPRO$\mathrm{\Delta }PRO$ is similar to ΔRQO$\mathrm{\Delta }RQO$
    ∴PR=RQ$\therefore PR=RQ$
    P Q = PR + RQ
    PQ=2PR=2×3400tan15∘$PQ=2PR=2\times 3400\tan {15}^{\circ }$
    PQ=6800×0.268=1822.4m$PQ=6800\times 0.268=1822.4\mathrm{m}$
    ∴$\therefore$ Speed of the aircraft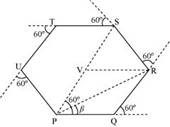 =distancetimeinterval=1822.410$=\frac{distance}{timeinterval}=\frac{1822.4}{10}$ = 182.24 m/s

15. 
    The path followed by the motorist is a regular hexagon with side 500 m, as shown in the given figure
    Let the motorist start from point P.
    The motorist takes the third turn at S.
    Magnitude of displacement = PS = PV + VS = 500 + 500 = 1000 m (∵PV=QR,VS=SR)$(\because PV=QR,VS=SR)$
    Total path length, d1 = PQ + QR + RS = 500 + 500 + 500 = 1500 m
    The motorist take the sixth turn at point P, which is the starting point
    ∴$\therefore$ Magnitude of displacement = 0
    Total path length, d2 = PQ + QR + RS + ST + TU + UP
    d2 = 500 + 500 + 500 + 500 + 500 = 3000 m
    The motorist takes the eight turn at point R
    ∴$\therefore$ Magnitude of displacement = PR
    PR=PQ2+QR2+2(PQ)⋅(QR)cos60∘−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$PR=\sqrt{P{Q}^2+Q{R}^2+2(PQ)\cdot (QR)\cos {60}^{\circ }}$
    PR=5002+5002+(2×500×500×cos60∘)−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√$PR=\sqrt{{500}^2+{500}^2+(2\times 500\times 500\times \cos {60}^{\circ })}$
    PR=250000+25000+(500000×12)−−−−−−−−−−−−−−−−−−−−−−−−−√$PR=\sqrt{250000+25000+\left(500000\times \frac{1}{2}\right)}$
    PR=866.03m$PR=866.03m$
    β=tan−1(500sin60∘500+500cos60∘)=30∘$\beta ={\tan }^{-1}\left(\frac{500\sin {60}^{\circ }}{500+500\cos {60}^{\circ }}\right)={30}^{\circ }$
    Therefore, the magnitude of displacement is 866.03 m at an angle of 30o with PR.
    Total path length = Circumference of the hexagon + PQ + QR
    Total path length= 6 ×$\times$ 500 + 500 + 500 = 4000 m
    The magnitude of displacement and the total path length corresponding to the required turns is shown in the given table

    Turn	Magnitude of displacement (m)	Total path length (m)
    Third	1000	1500
    Sixth	0	3000
    Eighth	866.03; 30o	4000