Mensuration - Solutions 2
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 11
Mensuration (Ex. 11.2)
NCERT Solutions
CHAPTER - 11
Mensuration (Ex. 11.2)
1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
Ans.
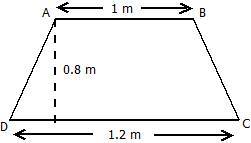
Parallel side of the trapezium AB =1m , CD = 1.2 m and height of the trapezium (AM) = 0.8 m
of the trapezium (AM) = 0.8 m

Parallel side of the trapezium AB =1m , CD = 1.2 m and height
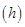 of the trapezium (AM) = 0.8 m
of the trapezium (AM) = 0.8 m
Area of top surface of the table = (sum of parallel sides) Height
= x (AB + CD) x AM
= 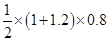
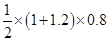
= 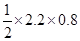
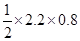
= 0.88 m2
Thus surface area of the table is 0.88 

2. The area of a trapezium is 34 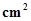 and the length of one of the parallel sides is 10 cm and its height is 4 cm.
and the length of one of the parallel sides is 10 cm and its height is 4 cm.
Find the length of the other parallel side.
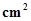 and the length of one of the parallel sides is 10 cm and its height is 4 cm.
and the length of one of the parallel sides is 10 cm and its height is 4 cm.
Find the length of the other parallel side.
Ans. Let the length of the other parallel side be = b cm
Length of one parallel side = 10 am and height 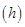 = 4 cm
= 4 cm
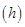 = 4 cm
= 4 cm
Area of trapezium = (sum of parallel sides) Height
=> 34 =(a+b)h
=> 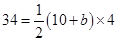
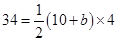
=> 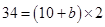
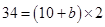
=> 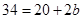
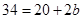
=> 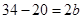
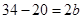
=> 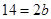
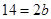
=> 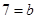
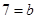
=> 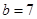
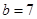
Hence another required parallel side is 7 cm.
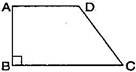
3. Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
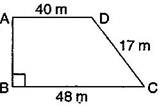
Ans. Given: BC = 48 m, CD = 17 m,

Ans. Given: BC = 48 m, CD = 17 m,
AD = 40 m and perimeter = 120 m
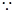 Perimeter of trapezium ABCD = Sum of all sides
Perimeter of trapezium ABCD = Sum of all sides
120 =(AB + BC + CD + DA)
120 = AB + 48 + 17 + 40
120 = AB + 105
(120 – 105) = AB
AB = 15 m
Now Area of the field = x(Sum of parallel sides) x Height
=x(BC+AD)xAB
= x(48+40)x15 m2
= x(88)x15 m2
=( 1320) m2
= 660 

Hence area of the field ABCD is 660 .
.
 .
.
4. The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
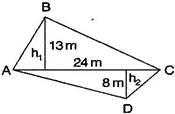
Ans. Here h1 = 13 m, h2 = 8 m and AC = 24 m

Ans. Here h1 = 13 m, h2 = 8 m and AC = 24 m
Area of quadrilateral ABCD = Area of  ABC + Area of
ABC + Area of 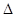 ADC
ADC
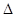 ABC + Area of
ABC + Area of 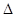 ADC
ADC
= 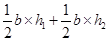
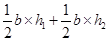
= 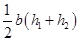
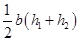
= x 24 (13 + 8) m2
=x24 (21) m2
=12 x 21 m2
=252 

Hence required area of the field is 252 

5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Ans. Given: d1 =7.5 cm and d2 = 12 cm
Area of rhombus = x(Product of digonals)
= x(d1 x d2 )
= x(7.5 x12) cm2
= 45 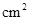
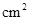
Hence area of rhombus is 45 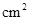 .
.
 .
.
6. Find the area of a rhombus whose side is 6 cm and whose altitude is 4 cm. If one of the diagonals is 8 cm long, find the length of the other diagonal.
Ans. Rhombus is also a kind of Parallelogram.
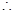 Area of rhombus= Base
Area of rhombus= Base  Altitude
Altitude= (6
 4) cm2
4) cm2= 24
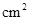
Also Area of rhombus = x (d1 x d2 )
24 = x(8 x d2 )
24 = 4 d2
cm = d2
d2 = 6 cm
24 = x(8 x d2 )
24 = 4 d2
cm = d2
d2 = 6 cm
Hence, the length of the other diagonal is 6 cm.
7. The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per 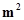 is ` 4.
is ` 4.
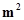 is ` 4.
is ` 4.
Ans. Here, d1 = 45 cm and d2 = 30 cm
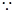 Area of one tile = x (d1 x d2 )
Area of one tile = x (d1 x d2 )
= x(45 x 30 )
=(1350)
= 675 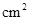
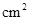
So, the area of one tile is 675 cm2
Area of 3000 tiles = 675  3000 cm2
3000 cm2
 3000 cm2
3000 cm2
= 2025000 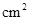
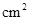
= m2
[1 cm = m, Here cm2 = Cm x cm = x m2 ]
[1 cm = m, Here cm2 = Cm x cm = x m2 ]
= 202.50 

 Cost of polishing the floor per sq. meter = Rs. 4
Cost of polishing the floor per sq. meter = Rs. 4 Cost of polishing the floor per 202.50 sq. meter =Rs. 4
Cost of polishing the floor per 202.50 sq. meter =Rs. 4  202.50 = Rs. 810
202.50 = Rs. 810
Hence the total cost of polishing the floor is Rs. 810.
8. Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the sidealong the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Ans.
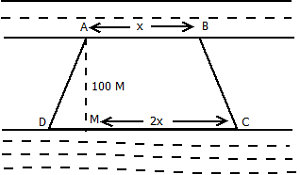
Given: Perpendicular distance (h) AM = 100 m

Given: Perpendicular distance (h) AM = 100 m
Area of the trapezium shaped field = 10500 

Let side along the road AB= 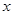 m
m
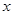 m
m
side along the river CD = m
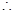 Area of the trapezium field = x (AB + CD) x AM
Area of the trapezium field = x (AB + CD) x AM
10500 = 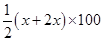
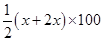
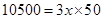
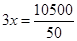
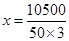
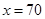 m
m
Hence the side along the river = 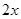 = (2
= (2  70) = 140 m.
70) = 140 m.
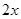 = (2
= (2  70) = 140 m.
70) = 140 m.
9. Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Ans.
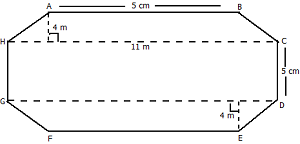
Given: Octagon having eight equal sides, each 5 m.

Given: Octagon having eight equal sides, each 5 m.
Construction: Join HC and GD It will divide the octagon into two equal trapezium.
And AM is perpendicular on HC and EN is perpendicular on GD
Area of trap. ABCD = Area of trap. GDFE ....................................(1)
Area of two trapeziums = (area of trap. ABCH + area of trap. GDFE)
= (area of trap. ABCH + area of trap. ABCH) (by statement 1).
= (2 x area of trap. ABCH )
= (2 x area of trap. ABCH )
= (2 x x (sum of parallel sides ) x height)
= (2 x x(AB + CH) x AM)
=(11 + 5 ) x 4 m2
=(16) x 4
= 64 

And Area of rectangle (HCDG ) = length  breadth
breadth
 breadth
breadth
= HC x HG = 11  5 = 55
5 = 55 
 5 = 55
5 = 55 
 Total area of octagon = Area of 2 Trapezium + Area of Rectangle
Total area of octagon = Area of 2 Trapezium + Area of Rectangle
= 64 m2 + 55 m2 = 119 

10. There is a pentagonal shaped park as shown in the figure. For finding its are a Jyoti and Kavita divided it in two different ways.
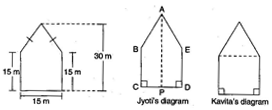
Find the area of this park using both ways. Can you suggest some other way of finding its area?

Find the area of this park using both ways. Can you suggest some other way of finding its area?
Ans. First way: By Jyoti’s diagram,
Area of pentagon = Area of trapezium ABCP + Area of trapezium AEDP
= 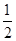 (AP + BC) x CP +
(AP + BC) x CP + 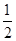 (ED + AP)
(ED + AP)  DP
DP
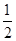 (AP + BC) x CP +
(AP + BC) x CP + 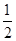 (ED + AP)
(ED + AP)  DP
DP
= 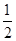 (30 + 15 ) x CP +
(30 + 15 ) x CP + 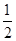 (15 + 30)
(15 + 30)  DP
DP
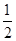 (30 + 15 ) x CP +
(30 + 15 ) x CP + 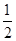 (15 + 30)
(15 + 30)  DP
DP
= 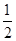 (30 + 15) (CP + DP)
(30 + 15) (CP + DP)
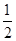 (30 + 15) (CP + DP)
(30 + 15) (CP + DP)
= 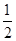
 45
45  CD
CD
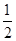
 45
45  CD
CD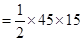
=337.5 m2
Second way: By Kavita’s diagram
Here, a perpendicular AM drawn to BE. AM = 30 – 15 = 15 m
Area of pentagon = Area of  ABE + Area of square BCDE
ABE + Area of square BCDE
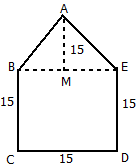
={ 15
15 15}+(15
15}+(15 15) m2
15) m2
 ABE + Area of square BCDE
ABE + Area of square BCDE
={
 15
15 15}+(15
15}+(15 15) m2
15) m2
= (112.5 + 225.0) m2
= 337.5 m2
Hence total area of pentagon shaped park = 337.5 .
.
 .
.
11. Diagram of the adjacent picture frame has outer dimensions = 24 cm  28 cm and inner dimensions 16 cm
28 cm and inner dimensions 16 cm  20 cm. Find the area of each section of theframe, if the width of each section is same.
20 cm. Find the area of each section of theframe, if the width of each section is same.
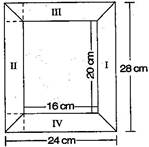
Ans. Here two of given figures (I) and (II) are similar in dimensions. And also figures (III) and (IV) are similar in dimensions.
 28 cm and inner dimensions 16 cm
28 cm and inner dimensions 16 cm  20 cm. Find the area of each section of theframe, if the width of each section is same.
20 cm. Find the area of each section of theframe, if the width of each section is same.
Ans. Here two of given figures (I) and (II) are similar in dimensions. And also figures (III) and (IV) are similar in dimensions.
 Area of figure (I) = Area of trapezium
Area of figure (I) = Area of trapezium
= 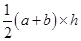 =
= 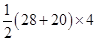
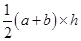 =
= 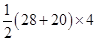
= 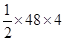 = 96
= 96 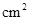
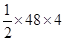 = 96
= 96 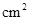
Also Area of figure (II) = 96 cm2
Now Area of figure (III)
Area of trapezium = 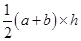
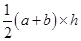
= 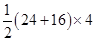
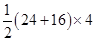
= 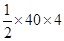
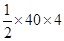
= 80 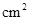
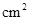
Also Area of figure (IV) = 80