Lines and Angles - Solutions 2
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 5 Lines and Angles (Ex. 5.2)
NCERT Solutions
Chapter 5 Lines and Angles (Ex. 5.2)
Question 1. State the property that is used in each of the following statements:
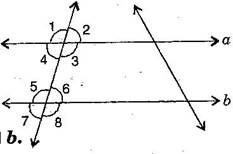

- If then 1 = 5.
- If 4 = 6, then
- If 4 + 5 + then
Answer: (i) Given, then 1 = 5 [Corresponding angles]
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
If two parallel lines are cut by a transversal, each pair of corresponding angles are equal in measure.
(ii) Given, 4 = 6, then [Alternate interior angles]
When a transversal cuts two lines such that pairs of alternate interior angles are equal, the lines have to be parallel.
When a transversal cuts two lines such that pairs of alternate interior angles are equal, the lines have to be parallel.
(iii) Given, 4 + 5 = then [Co-interior]
When a transversal cuts two lines, such that pairs of interior angles on the same side of transversal are supplementary, the lines have to be parallel.
When a transversal cuts two lines, such that pairs of interior angles on the same side of transversal are supplementary, the lines have to be parallel.
Question 2. In the adjoining figure, identify:
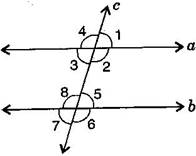

- the pairs of corresponding angles.
- the pairs of alternate interior angles.
- the pairs of interior angles on the same side of the transversal.
- the vertically opposite angles.
Answer: (i) The pairs of corresponding angles:
1, 5; 2, 6; 4, 8 and 3, 7
(ii) The pairs of alternate interior angles are:
3, 5 and 2, 8
(iii) The pair of interior angles on the same side of the transversal:
3, 8 and 2, 5
(iv) The vertically opposite angles are:
1, 3; 2, 4; 6, 8 and 5, 7
Question 3. In the adjoining figure, Find the unknown angles.
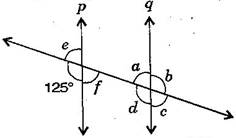

Answer: Given, and cut by a transversal line.
[Linear pair]
……….(i)
Now [Vertically opposite angles]
Also [Alternate interior angles]
[Linear pair]
[From eq. (i)]
Now and [Vertically opposite angles]
Thus, and
Question 4. Find the values of in each of the following figures if
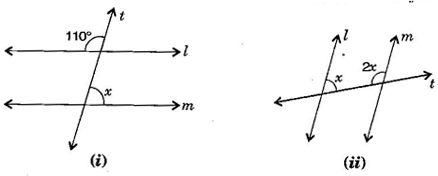
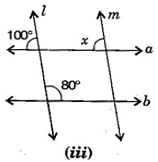
Answer: (i) Given, and is transversal line.


Answer: (i) Given, and is transversal line.
Interior vertically opposite angle between lines and
[Supplementary angles]
(ii) Given, and is transversal line.
[Interior opposite angles]
(iii) Given, and .
[Corresponding angles]
Question 5. In the given figure, the arms of two angles are parallel. If then find:
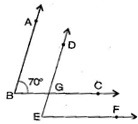
(i) DGC

(i) DGC
(ii) DEF
Answer: (i) Given, AB DE and BC is a transversal line and
ABC = DGC [Corresponding angles]
DGC = ……….(i)
DGC = ……….(i)
(ii) Given, BC EF and DE is a transversal line and
DGC = DEF [Corresponding angles]
DEF = [From eq. (i)]
Question 6. In the given figures below, decide whether is parallel to m.
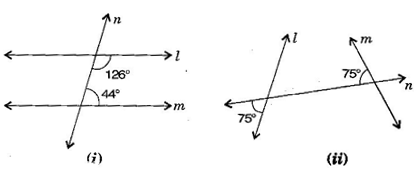
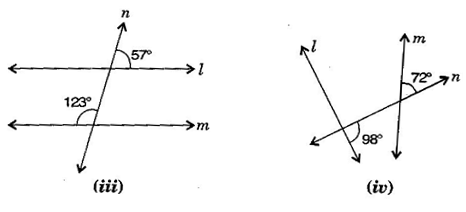
Answer: (i)


Answer: (i)
is not parallel to because sum of interior opposite angles should be
(ii)
is not parallel to because sum of angles does not obey the property of parallel lines.
(iii)
is parallel to due to supplementary angles property of parallel lines.
(iv)
is not parallel to because sum of angles does not obey the property of parallel lines.
