Linear Equations in One Variable - Worksheets

CBSE Worksheet-01
Class 08 - Mathematics (Linear Equations in One Variable)

---

General Instructions: All questions are compulsory. Q.1 to Q.2 carries one mark each. Q.3 to Q.7 carries two marks each. Q.8 and Q.9 carries three marks each. Q.10 to Q.12 carries four marks each.

---

1. 1. Two numbers are in the ratio 6:5. If the sum of the numbers is 110, find the numbers.
   2. Hari's father gave him Rs 70. Now, he has Rs 130. How much money did Hari have in the beginning?
2. 1. What is the length of the stick, if 16$\frac{1}{6}$ of the length of a stick is 5cm.
   2. Five times Raju' pocket money is Rs 80. What is his pocket money?
3. State whether the following statements are True or False:
   1. Sum of two numbers is 95. If one exceeds the other by 15 then the larger number is 40.
   2. x = 4 is the root of 12x + 8 = 56.
   3. The rational number is −12$\frac{-1}{2}$, when you multiply it by 25$\frac{2}{5}$ and 23$\frac{2}{3}$ is added to the product, you get 715$\frac{7}{15}$.
   4. m=57$m=\frac{5}{7}$, for m−m−12=1−m−23$m-\frac{m-1}{2}=1-\frac{m-2}{3}$.
4. Fill in the blanks:-
   1. The other name of a solution of an equation is _____.
   2. A polynomial of degree 1 is called _____ polynomial.
   3. The literal symbol which takes on various numerical values is called a _____.
   4. A combination of constants and variables, connect by basic operations is called an _____.
5. Math the following:

   Column A	Column B
   a. x−3x+1=12$\frac{x-3}{x+1}=\frac{1}{2}$, x = ?	p. t = 50
   b. xx−3=2$\frac{x}{x-3}=2$, x = ?	q. z = 4
   c. t5=10$\frac{t}{5}=10$, t = ?	r. x = 7
   d. 6 = z + 2, z = ?	s. x = 6

6. Solve the following equation :5t – 3 = 3t – 5
7. Solve the following equation : 37+x=177$\frac{3}{7}+x=\frac{17}{7}$.
8. Solve the following linear equation :x−53=x−35$\frac{x-5}{3}=\frac{x-3}{5}$
9. Solve the following equation : x3+1=715$\frac{x}{3}+1=\frac{7}{15}$
10. The numerator of a fraction is 2 less than the denominator. If 1 is added to its denominator, it becomes 12$\frac{1}{2}$. Find fraction.
11. If you subtract 12$\frac{1}{2}$ from a number and multiply the result 12$\frac{1}{2}$, you get 18$\frac{1}{8}$. What is the number ?
12. Half of a herd of deer are grazing in the field and three fourths of the remaining are playing nearby. The rest 9 are drinking water from the pond. Find the number of deer in the herd.

CBSE Worksheet-01
Class 08 - Mathematics (Linear Equations in One Variable)
Solution

---

1. 1. Let the numbers be 6x and 5x respectively.
      According to the question.
      6x + 5x = 110
      11x = 110
      11x11=11011$\frac{11x}{11}=\frac{110}{11}$ [Dividing both sides by 11]
      ∴$\therefore$ x = 10
      So, the numbers are 6x=6×10=60$6x=6\times 10=60$
      and 5x=5×10=50$5x=5\times 10=50$
   2. Let, the amount he had = Rs x
      Money his father gave him = Rs 70
      So, x + 70 = 130
      ∴$\therefore$ x = 130 - 70
      x = 60
      So, Hari had Rs 60 in the beginning.
2. 1. Let the length of the stick be l cm.
      So, 16l=5cm$\frac{1}{6}l=5cm$
      l=5×6$l=5\times 6$
      ∴$\therefore$ l = 30 cm.
   2. Let Raju's pocket money be x rupees.
      So, 5x = 80
      x=805$x=\frac{80}{5}$
      ∴$\therefore$ x = 16 So, raju's pocket money is Rs. 16.
3. 1. False
   2. True
   3. True
   4. False
4. 1. Root
   2. Linear
   3. Variable
   4. algebraic expression
5. 1. - r
   2. - s
   3. - p
   4. - q
6. 5t – 3 = 3t – 5
   5t – 3t = -5 + 3 . . . . [Transposing 3t to L.H.S. and –3 to R.H.S.]
   2t = –2
   ∴ t=−22$t=-\frac{2}{2}$. . . . [Dividing both sides by 2]
   ∴ t = –1 this is the required solution.
7. 37+x=177$\frac{3}{7}+x=\frac{17}{7}$
   ∴ x=177−37$x=\frac{17}{7}-\frac{3}{7}$. . . . [Transposing 37$\frac{3}{7}$ to R.H.S.]
   ∴ x=17−37$x=\frac{17-3}{7}$
   ∴ x=147$x=\frac{14}{7}$
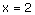   ∴  this is the required solution.
   Verification
   L.H.S. =37+x=37+2=177$=\frac{3}{7}+x=\frac{3}{7}+2=\frac{17}{7}$ R.H.S.
8. x−53=x−35$\frac{x-5}{3}=\frac{x-3}{5}$ It is a linear equation since if involves linear expressions only.
   ∴ x3−53=x5−35$\frac{x}{3}-\frac{5}{3}=\frac{x}{5}-\frac{3}{5}$
   ∴ x3−x5=35+53$\frac{x}{3}-\frac{x}{5}=\frac{3}{5}+\frac{5}{3}$ . . . . [Transposing x5$\frac{x}{5}$ to L.H.S. and −53$\frac{-5}{3}$ to R.H.S.]
   ∴ 5x−3x15=25−915$\frac{5x-3x}{15}=\frac{25-9}{15}$
   ∴ 2x5=1615$\frac{2x}{5}=\frac{16}{15}$
   ∴ x=1615×152$x=\frac{16}{15}\times \frac{15}{2}$ . . . . [Multiplying both sides by 152$\frac{15}{2}$]
   ∴ x = 8 this is the required solution.
   Verification
   L.H.S. =8−53=33=1$=\frac{8-5}{3}=\frac{3}{3}=1$
   R.H.S. =8−35=55=1$=\frac{8-3}{5}=\frac{5}{5}=1$
   Therefore, L.H.S. = R.H.S.
9. x3+1=715$\frac{x}{3}+1=\frac{7}{15}$
   ∴ x3=715−1$\frac{x}{3}=\frac{7}{15}-1$ [Transposing 1 to R.H.S. ]
   ∴ x3=7−1515$\frac{x}{3}=\frac{7-15}{15}$
   ∴ x3=−815$\frac{x}{3}=\frac{-8}{15}$
   ∴ x=(−815)×3$x=\left(-\frac{8}{15}\right)\times 3$. . . . [Multiplying both sides by 3]
   ∴ x=−85$x=\frac{-8}{5}$. . . . this is the required solution.
   Verification
   L.H.S. =x3+1$=\frac{x}{3}+1$
   =13(−85)+1$=\frac{1}{3}\left(\frac{-8}{5}\right)+1$
   =−815+1$=\frac{-8}{15}+1$
   =−8+1515$=\frac{-8+15}{15}$
   =715$=\frac{7}{15}$
   = R.H.S.
10. Let the denominator of the fraction be x then, numerator is x - 2
    and the fraction becomes =x−2x$=\frac{x-2}{x}$
    when 1 is added to the denominator, the fraction becomes 12$\frac{1}{2}$
    So, x−2x+1=12$\frac{x-2}{x+1}=\frac{1}{2}$
    By cross multiplication, we have
    2(x - 2) = x + 1
    2x - 4 = x + 1
    2x - x = 1 + 4
    ∴$\therefore$ x = 5
    So, the fraction is x−2x=5−25$\frac{x-2}{x}=\frac{5-2}{5}$
    i.e. =35$=\frac{3}{5}$
11. Let the number be x
    According to the question,
    12(x−12)=18$\frac{1}{2}\left(x-\frac{1}{2}\right)=\frac{1}{8}$
    ∴ 12(2x−12)=18$\frac{1}{2}\left(\frac{2x-1}{2}\right)=\frac{1}{8}$
    ∴ 2x−14=18$\frac{2x-1}{4}=\frac{1}{8}$
    ∴ 2x−14×8=18×8$\frac{2x-1}{4}\times 8=\frac{1}{8}\times 8$. . . . [Multiplying both sides by 8]
    ∴ (2x – 1) 2 = 1
    ∴ 4x – 2 = 1
    ∴ 4x = 1 + 2 . . . . [Transposing – 2 to R.H.S.]
    ∴ 4x = 3
    ∴ x=34$x=\frac{3}{4}$. . . . [Dividing both sides by 4]
    Hence, the desired number is 34$\frac{3}{4}$.
    Verification
    12(34−12)$\frac{1}{2}\left(\frac{3}{4}-\frac{1}{2}\right)$
    =12(3−24)$=\frac{1}{2}\left(\frac{3-2}{4}\right)$
    =12(14)$=\frac{1}{2}\left(\frac{1}{4}\right)$
    =18$=\frac{1}{8}$
12. Let the number of deer in the herd be x.
    Then, number of deer grazing in the field =x2$=\frac{x}{2}$
    ∴ Number of remaining deer =x−x2=x2$=x-\frac{x}{2}=\frac{x}{2}$
    ∴ Number of deer playing nearby =3(x/2)4=3x8$=\frac{3(x/2)}{4}=\frac{3x}{8}$
    Number of deer drinking water from the pound =x−(x2+3x8)$=x-\left(\frac{x}{2}+\frac{3x}{8}\right)$
    =x−(4x+3x8)$=x-\left(\frac{4x+3x}{8}\right)$
    =x−7x8$=x-\frac{7x}{8}$
    =8x−7x8$=\frac{8x-7x}{8}$
    =x8$=\frac{x}{8}$
    According to the question,
    x8=9$\frac{x}{8}=9$
    ∴ x = 9 × 8 . . . . [ Multiplying both sides by 8]
    ∴ x = 72 hence, the number of deer in the herd is 72
    Verification
    722=36$\frac{72}{2}=36$
    34(36)=27$\frac{3}{4}(36)=27$
    72 – (36 + 27) = 72 – 63 = 9 hence, the result is verified.