Laws of Motion - Test Papers

 CBSE Test Paper 01

Chapter 5 Laws of Motion

---

1. A monkey of mass 40 kg climbs on a rope which can stand a maximum tension of 600 N. What is the tension in the rope if the monkey falls down the rope nearly freely under gravity? 1

   1. 400 N
   2. 200 N
   3. 0 N
   4. 600 N

2. A constant retarding force of 50 N is applied to a body of mass 20 kg moving initially with a speed of 15 m s−1${\mathrm{s}}^{-1}$. How long does the body take to stop? 1

   1. 7.0 s
   2. 4.0 s
   3. 6.0 s
   4. 5.0 s

3. Rolling friction is 1

   1. greater than static friction
   2. less than static friction
   3. greater than or equal to static
   4. equal to static friction

4. A nucleus is at rest in the laboratory frame of reference. If it disintegrates into two smaller nuclei 1

   1. the products must move at an angle in same direction.
   2. the products must move in same direction.
   3. the products must move at an angle in opposite directions.
   4. the products must move in opposite directions.

5. force is required 1

   1. only to keep an object moving
   2. only to stop a moving object
   3. to start a stationary object and to stop a moving object
   4. only to start a stationary object moving

6. Does inertia of a body depend on any factor other than mass? 1

7. Why is it desired to hold a gun tight to one’s shoulder when it is being fired? 1

8. If force is acting on a moving body perpendicular to the direction of motion, then what will be its effect on the speed and direction of the body? 1

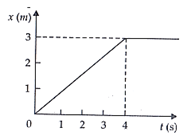
9. The position-time graph of a body of mass 2 kg is as given in Figure. What is the impulse on the body at t = 0 s and t = 4 s? 2
   

10. How does banking of roads reduce wear and tear of the tyres? 2

11. What do you mean by inertia of motion? Give an example to illustrate it. 2

12. In a circus a motorcyclist driving in vertical loops inside a 'death-well' (a hollow spherical chamber with holes, so the spectators can watch from outside). Explain clearly why the motorcyclist does not drop down when he is at the uppermost point, with no support from below. What is the minimum speed required at the uppermost position to perform a vertical loop if the radius of the chamber is 25 m? 3

13. A 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed? 3

14. Three identical blocks each having a mass m, are pushed by a force F on a frictionless table as shown in figure
    
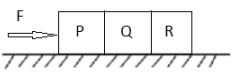
    What is the acceleration of the blocks? What is the net force on the block P? What force does P apply on Q. What force does Q apply on R? 3

15. A body of mass 400 gm moving initially with a constant speed of 36 km h-1 towards the north is subjected to a constant force of 8.0 N directed towards the south for half of a minute. Beyond that time the body continues its motion with uniform velocity. No other forces are acting on the body throughout its motion. Take the instant the force is applied to be at t = 0 s, the position of the body at that time to be x = 0 m. Find out its position at t = -5 s, 25 s and 100 s respectively applying Newton's equations of motion. 5

CBSE Test Paper 01
Chapter 5 Laws of Motion

---

Answer

1. 3. 0 N
      Explanation: When the monkey fall down down the rope nearly free under the gravity, a=g, so
      T = m(g - a) = m(g - g) = 0N

2. 3. 6.0 s
      Explanation: F=mdvdt$F=m\frac{dv}{dt}$
      dt=mdvF=20×1550=6s$dt=m\frac{dv}{F}=20\times \frac{15}{50}=6s$

3. 2. less than static friction
      Explanation: As the area of contact is less in the case of rolling than in the case of sliding. In rolling surface of contact do not rub each other. The velocity of the point of contact with respect to the surface remains zero all the time although the Centre of mass of the wheel moves forward. Hence rolling friction is negligible in comparison to static friction.

4. 4. the products must move in opposite directions.
      Explanation: Let, M = mass of nucleus at rest . m1 and m2 are masses of two smaller nuclei. v1 and v2 are the velocities of respective masses
      Now, According to the law of conservation of momentum,
      Initial momentum before disintegration = final momentum after disintegration
      m1v1+m2v2=0$m_1{v}_1+m_2{v}_2=0$
      v2=−m2m1⋅v1$v_2=-\frac{m_2}{m_1}\cdot v_1$
      As masses m1$m_1$and m2$m_2$ cannot be negative, v1$v_1$ and v2$v_2$ having opposite signs and so the two smaller nuclei move in opposite directions.

5. 3. to start a stationary object and to stop a moving object
      Explanation: force is required to start a stationary object and to stop a moving object due to inertia. Inertia is a property of matter by which it continues in its existing state of rest or uniform motion in a straight line, unless that state is changed by an external force. This is also called law of inertia or newton's first law of motion

6. No, it does not depend on any other factor except mass.

7. If m, M, v and V are the mass of a bullet, mass of the gun, velocity of the bullet and recoil velocity of the gun respectively, then according to the law of conservation of linear momentum V = - mv/M. With this velocity the gun will recoil during firing. This backward push is so hard that it can displace our shoulder and injure us. That is why the gun must be held tightly against the shoulder because gun and the shoulder constitute one system of greater mass so the back kick will be less.

8. No change in speed, but there can be change in the direction of motion. Let's start with an example. When a body is in a uniform circular motion, the centripetal acceleration or centripetal force always acts perpendicular to the linear velocity of the body at any point of its trajectory. In this case the velocity of the body keeps on changing its direction time to time, but speed remains same.

9. Mass of body (m) = 2 kg at t =0.. Initial velocity (v1) is zero, V1 = 0 from t≥0 to t≤4,(x−t)$t\ge 0\text{ to }t\le 4,(x-t)$ graph is straight line. So the velocity (v) of body is constant.
   v2=tanθ=34=0.75m/s$v_2=\tan \theta =\frac{3}{4}=0.75\mathrm{m}/\mathrm{s}$
   At t≥4$t\ge 4$ the slope of the graph is zero so velocity V3 = 0
   Impulse =F⃗ t=d⃗ pdt⋅dt=dp⃗ $=\overrightarrow{F}t=\frac{\overrightarrow{d}p}{dt}\cdot dt=d\overrightarrow{p}$
   Impulse = Change in momentum
   Impulse at t = 0: = 2[0.75 – 0] = 1.50 kg ms-1 (increased)
   Impulse at t = 4: =m(v3−v2)$=m\left(v_3-v_2\right)$ =2[0 – 0.75]
   Impulse at t = 4: = -1.50 kg ms-1
   So impulse at t = 0 increases by + 1.5 kg ms-1 ­and at t = 4 it decreased by (-1.5 kg ms-1).

10. When a curved road is unbanked force of friction between the tyres and the road provides the necessary centripetal force. Friction has to be increased which will cause wear and tear. But when the curved road is banked, a component of normal reaction of the ground provides the necessary centripetal force which reduces the wear and tear of the tyres.

11. Inertia of motion is the tendency of a body to maintain its state of uniform motion. As an illustration, we observe that a person jumping out of a running train or bus falls with his head in forward direction due to the inertia of motion. Similarly, passengers experience a forward push when the driver of a bus running at high speed suddenly applies brakes.

12. When the motorcyclist is at the highest point of the death-well, the normal reaction R on the motorcyclist by the ceiling of the chamber acts downwards. His weight mg also acts downwards. These two forces are balanced by the outward centrifugal force acting on him. This situation is shown in the following figure.
    
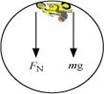
    The net force acting on the motorcyclist is the sum of the normal force (FN) and the force due to gravity (Fg = mg).
    The equation of motion for the centripetal acceleration ac, can be written as:
    Fnet = mac
    FN + Fg = mac
    Fx+mg=mv2r$F_x+mg=\frac{m{v}^2}{r}$
    Here,v is the speed of the motorcyclist and m is the mass of the motorcyclist(including the mass of the motor cycle). Because of the balancing of the forces, the motorcyclist does not fall down. The minimum speed required to perform a vertical loop is given by above equation when FN=0$F_N=0$
    mg=mv2minr$mg=\frac{m{v}_{min}^2}{r}$
    ∴vmin=rg−−√$\therefore v_{min}=\sqrt{rg}$
    =25×10−−−−−−√=15.8m/s$=\sqrt{25\times 10}=15.8\mathrm{m}/\mathrm{s}$

13. Mass of the man, m = 70 kg
    Radius of the drum, r = 3 m
    Coefficient of friction, μ$\mu$ = 0.15
    Frequency of rotation, v = 200 rev/min =20060=103rev/s$=\frac{200}{60}=\frac{10}{3}rev/s$
    The normal reaction N provides the necessary centripetal force N = mv2/r = mrω2
    The frictional force balances the weight of the man, fs = mg
    Now, the man will remain stuck to the wall after the floor has been removed when
    fs ≤ μ N
    That is,mg ≤ μ N
    mg ≤ μmrω2
    ω2 ≥ g/μr
    The minimum angular speed is given as:
    ωmin=gμr−−√${\omega }_{min}=\sqrt{\frac{g}{\mu r}}$
    =100.15×3−−−−−√=4.71rads−1$=\sqrt{\frac{10}{0.15\times 3}}=4.71rad{s}^{-1}$

14. If a is the acceleration of the whole system containing three blocks, then F = mass of the system ×$\times$ acceleration of the system = (m + m + m) ×$\times$ a
    ⇒$\Rightarrow$ F = 3 ma
    ∴a=F3m$\therefore a=\frac{F}{3m}$

    1. Net force on P, F1=ma=m×F3m$F_1=ma=m\times \frac{F}{3m}$
       ⇒F1=F3$\Rightarrow F_1=\frac{F}{3}$
    2. Force applied on Q by P = reaction force on P by Q,
       F2 = (m + m)a [since, the reaction force comes due to masses of Q and R]
       ∴F2=2m×a=2m×F3m$\therefore F_2=2m\times a=2m\times \frac{F}{3m}$
       ∴F2=2F3$\therefore F_2=\frac{2F}{3}$
    3. Force applied on R by Q = reaction force on Q by R,
       F3=m×a=m×F3m$F_3=m\times a=m\times \frac{F}{3m}$
       ∴F3=F3$\therefore F_3=\frac{F}{3}$

15. Mass of the body, m = 400 gm = 0.40 kg
    Initial speed of the body, u = 36 km/h = (36×5/18) = 10 m/s, due north
    Force acting on the body, F = -8.0 N due north
    Acceleration produced in the body, a=Fm=−8.00.40=−20m/s2$a=\frac{F}{m}=\frac{-8.0}{0.40}=-20m/s^2$

    1. At t = -5 s
       Acceleration, a' = 0 and initial velocity, u = 10 m/s. Both are acting in the same direction i.e. due north. Applying Newton's second equation of motion,
       s=ut+12a′t2$s=ut+\frac{1}{2}{a}^{\mathrm{\prime }}{t}^2$
       =10×(−5)=−50m$=10\times (-5)=-50\mathrm{m}$
    2. At t = 25 s
       Acceleration, a'' = -20 m/s2 and initial velocity, u = 10 m/s. Here also both are acting towards north. Applying Newton's second equation of motion,
       s′=ud′+12a′′t2$s^{\mathrm{\prime }}=u{d}^{\mathrm{\prime }}+\frac{1}{2}{a}^{"}{t}^2$
       =10×25+12×(−20)×(25)2$=10\times 25+\frac{1}{2}\times (-20)\times (25{)}^2$
       = 250 - 6250 = -6000m
    3. At t = 100 s
       For 0≤t≤30s$0\le t\le 30s$
       During this time interval the body will continue its motion under the mentioned force i.e. Acceleration, a= -20 m/s2
       Initial velocity, u = 10 m/s. Both of them are acting due north. Now here also applying Newton's second equation of motion,
       s2=ut+12a′′t2$s_2=ut+\frac{1}{2}{a}^{\mathrm{\prime }\mathrm{\prime }}{t}^2$
       =10×30+12×(−20)×(30)2$=10\times 30+\frac{1}{2}\times (-20)\times (30{)}^2$
       = 300 - 9000 = -8700 M
       For 30′<t≤100s${30}^{\mathrm{\prime }}<t\le 100s$
       During this time interval the action of the force will no longer present. So in this part of time there will only be the uniform velocity. The velocity gained by the body after 30 s will act here as the uniform or constant velocity. As per the Newton's first equation of motion, for t = half of a minute = 30 s, final velocity is given as:
       v = u + at
       = 10 + (-20) ×$\times$ 30 = -590 m/s, due north
       Velocity of the body after 30 s = -590 m/s, acceleration = 0
       For motion between 30 s to 100 s, the body will continue its journey with uniform velocity, i.e., in 70 s:
       s2=vt+12a′′t2$s_2=vt+\frac{1}{2}{a}^{"}{t}^2$
       =−590×70=−41300m$=-590\times 70=-41300m$
       =−590×70=−41300m$=-590\times 70=-41300\mathrm{m}$
       ∴$\therefore$ Total distance, s" = s1 + s2 = - 8700 - 41300 = - 50000 m