Direct and Inverse Proportions - Solutions 1
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 13
Direct and Inverse Proportions (Ex. 13.1)
NCERT Solutions
CHAPTER - 13
Direct and Inverse Proportions (Ex. 13.1)
1. Following are the car parking charges near a railway station upto:
4 hours Rs.60
8 hours Rs.100
12 hours Rs.140
24 hours Rs.180

Check if the parking charges are in direct proportion to the parking time.
Ans. Charges per hour:
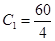 = Rs.15
= Rs.15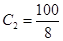 = Rs.12.50
= Rs.12.50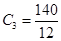 = Rs.11.67
= Rs.11.67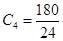 = Rs.7.50
= Rs.7.50
Here, the charges per hour are not same, i.e.,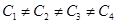
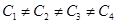
Therefore, the parking charges are not in direct proportion to the parking time.
2. A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.

Ans. Let the ratio of parts of red pigment and parts of base be 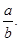
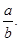
Here 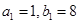
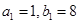

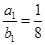 =
= 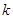 (say)
(say)
When 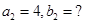
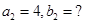
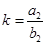

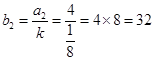
When 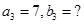
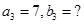
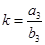

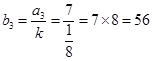
When 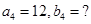
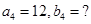
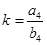

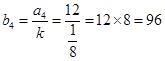
When 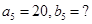
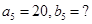
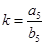

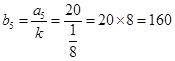

3. In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
Ans. Let the parts of red pigment mix with 1800 mL base be 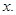
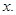

Since it is in direct proportion.
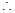
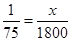

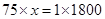

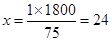 parts
parts
Hence with base 1800 mL, 24 parts red pigment should be mixed.
4. A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Ans. Let the number of bottles filled in five hours be 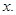
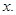
| Hours | 6 | 5 |
| Bottles | 840 | x |
Here ratio of hours and bottles are in direct proportion.
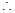
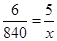

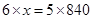

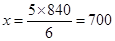 bottles
bottles
Hence machine will fill 700 bottles in five hours.
5. A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
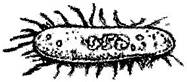
Ans.Let Actual length of bacteria be 'a'
It is enlarged 50,000 times so 50000 x a = 5 cm
Actual length of bacteria
= 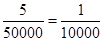 cm =
cm =  cm
cm
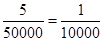 cm =
cm = 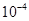 cm
cm
Let enlarged length of bacteria be 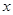
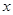
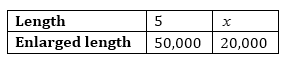
Here length and enlarged length of bacteria are in direct proportion.
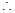
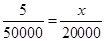

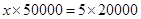

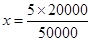 = 2 cm
= 2 cm
Hence the enlarged length of bacteria is 2 cm.
6. In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?

Ans. Let the length of model ship be 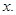
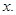

Here length of mast and actual length of ship are in direct proportion.
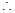
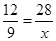

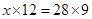

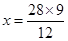 = 21 cm
= 21 cm
Hence length of the model ship is 21 cm.
7. Suppose 2 kg of sugar contains 9 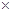
 crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
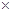
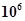 crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?
Ans. (i) Let sugar crystals be 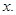
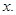

Here weight of sugar and number of crystals are in direct proportion.
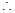
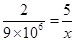

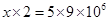

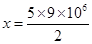
= 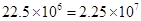
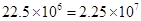
Hence the number of sugar crystals is 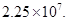
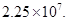

(ii) Let sugar crystals be 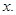
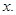
Here weight of sugar and number of crystals are in direct proportion.
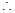
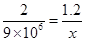

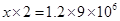

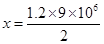
= 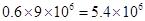
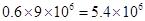
Hence the number of sugar crystals is 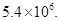
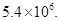
8. Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
Ans. Let distance covered in the map be 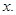
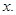

Here actual distance and distance covered in the map are in direct proportion.
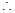
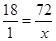

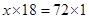

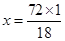 = 4 cm
= 4 cm
Hence distance covered in the map is 4 cm.
9. A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (i) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5 m long.
Ans. Here height of the pole and length of the shadow are in direct proportion.
And 1 m = 100 cm
5 m 60 cm = 5 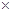 100 + 60 = 560 cm
100 + 60 = 560 cm
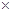 100 + 60 = 560 cm
100 + 60 = 560 cm
3 m 20 cm = 3 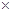 100 + 20 = 320 cm
100 + 20 = 320 cm
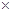 100 + 20 = 320 cm
100 + 20 = 320 cm
10 m 50 cm = 10 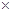 100 + 50 = 1050 cm
100 + 50 = 1050 cm
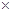 100 + 50 = 1050 cm
100 + 50 = 1050 cm
5 m = 5 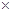 100 = 500 cm
100 = 500 cm
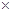 100 = 500 cm
100 = 500 cm
(i) Let the length of the shadow of another pole be 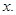

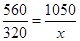

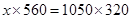

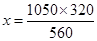 = 600 cm = 6 m
= 600 cm = 6 m
Hence length of the shadow of another pole is 6 m.
(ii) Let the height of the pole be 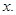
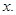

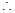
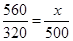

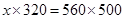

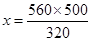
= 875 cm = 8 m 75 cm
Hence height of the pole is 8 m 75 cm.
10. A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Ans. Let distance covered in 5 hours be 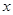 km.
km.
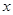 km.
km. 1 hour = 60 minutes
1 hour = 60 minutes 5 hours = 5
5 hours = 5 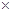 60 = 300 minutes
60 = 300 minutes
Here distance covered and time are in direct proportion.
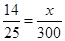

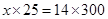

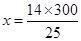 = 168 km
= 168 km