Cubes and Cube Roots - Solutions 2
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 7
Cubes and Cube Roots (Ex. 7.2)
NCERT Solutions
CHAPTER - 7
Cubes and Cube Roots (Ex. 7.2)
1. Find the cube root of each of the following numbers by prime factorization method:
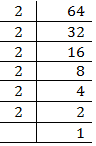
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Ans. (i) 64
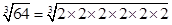
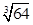 =
= 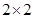 = 4
= 4

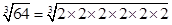
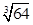 =
= 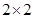 = 4
= 4
(ii) 512

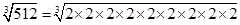
=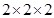 = 8
= 8

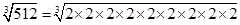
=
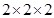 = 8
= 8
(iii) 10648
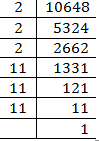
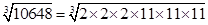
=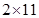 = 22
= 22

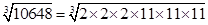
=
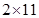 = 22
= 22
(iv) 27000
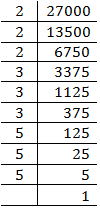
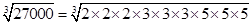
= = 30
= 30

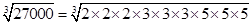
=
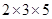 = 30
= 30
(v) 15625
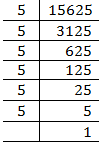
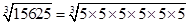
=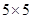 = 25
= 25

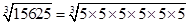
=
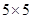 = 25
= 25
(vi) 13824
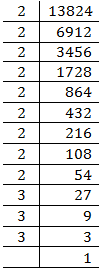
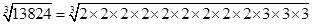
=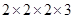 = 24
= 24

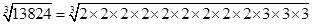
=
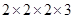 = 24
= 24
(vii) 110592
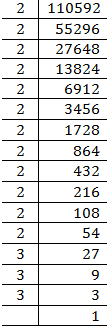
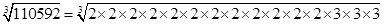
=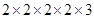 = 48
= 48

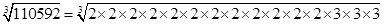
=
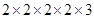 = 48
= 48
(viii) 46656
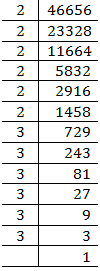
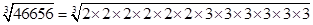
=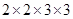 = 36
= 36

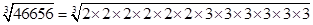
=
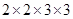 = 36
= 36
(ix) 175616
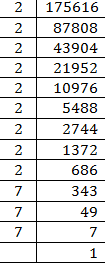
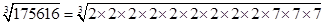
=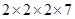 = 56
= 56

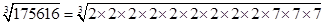
=
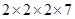 = 56
= 56
(x) 91125
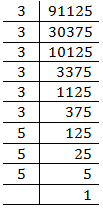
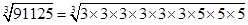
=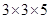 = 45
= 45

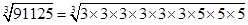
=
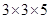 = 45
= 45
2. State true or false:
(i) Cube of any odd number is even.
(ii) A perfect cube does not end with two zeroes.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
(ii) A perfect cube does not end with two zeroes.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Ans. (i) False
Since,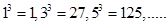 are all odd.
are all odd.
Since,
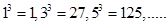 are all odd.
are all odd.
(ii) True
Since, a perfect cube ends with three zeroes.
e.g.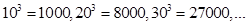 so on
so on
Since, a perfect cube ends with three zeroes.
e.g.
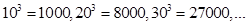 so on
so on
(iii) False
Since,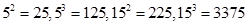
(Did not end with 25)
Since,
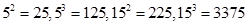
(Did not end with 25)
(iv) False
Since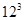 = 1728
= 1728
[Ends with 8]
And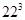 = 10648
= 10648
[Ends with 8]
Since
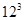 = 1728
= 1728[Ends with 8]
And
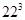 = 10648
= 10648[Ends with 8]
(v) False Since 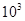 = 1000
= 1000
[Four digit number]
And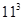 = 1331
= 1331
[Four digit number]
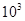 = 1000
= 1000[Four digit number]
And
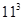 = 1331
= 1331[Four digit number]
(vi) False Since 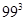 = 970299
= 970299
[Six digit number]
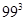 = 970299
= 970299[Six digit number]
(vii) True
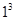 = 1
= 1
[Single digit number]
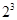 = 8
= 8
[Single digit number]
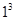 = 1
= 1[Single digit number]
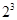 = 8
= 8[Single digit number]
3. You are told that 1,331 is a perfect cube. Can you guess without factorization what is its cube root? Similarly guess the cube roots of 4913, 12167, 32768.
Ans. We know that 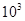 = 1000 and Possible cube of
= 1000 and Possible cube of 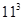 = 1331
= 1331
Since, cube of unit’s digit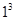 = 1
= 1
Therefore, cube root of 1331 is 11.
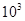 = 1000 and Possible cube of
= 1000 and Possible cube of 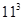 = 1331
= 1331Since, cube of unit’s digit
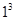 = 1
= 1Therefore, cube root of 1331 is 11.
4913
We know that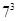 = 343
= 343
Next number comes with 7 as unit place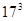 = 4913
= 4913
Hence, cube root of 4913 is 17.
We know that
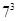 = 343
= 343Next number comes with 7 as unit place
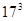 = 4913
= 4913Hence, cube root of 4913 is 17.
12167
We know that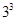 = 27
= 27
Here in cube, ones digit is 7
Now next number with 3 as ones digit
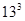 = 2197
= 2197
And next number with 3 as ones digit
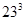 = 12167
= 12167
Hence cube root of 12167 is 23.
We know that
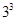 = 27
= 27Here in cube, ones digit is 7
Now next number with 3 as ones digit
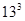 = 2197
= 2197And next number with 3 as ones digit
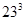 = 12167
= 12167Hence cube root of 12167 is 23.
32768
We know that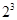 = 8
= 8
Here in cube, ones digit is 8
Now next number with 2 as ones digit
We know that
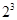 = 8
= 8Here in cube, ones digit is 8
Now next number with 2 as ones digit
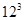 = 1728
= 1728And next number with 2 as ones digit
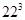 = 10648
= 10648And next number with 2 as ones digit
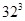 = 32768
= 32768Hence cube root of 32768 is 32.
