Cubes and Cube Roots - Solutions 1
CBSE Class –VIII Mathematics
NCERT Solutions
CHAPTER - 7
Cubes and Cube Roots (Ex. 7.1)
NCERT Solutions
CHAPTER - 7
Cubes and Cube Roots (Ex. 7.1)
1. Which of the following numbers are not perfect cubes:
(i) 216 (ii) 128 (iii) 1000 (iv) 100 (v) 46656
Ans. (i) 216
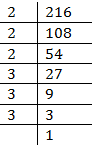
Prime factors of 216 =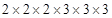 
Here all factors are in groups of 3’s (in triplets)
Therefore, 216 is a perfect cube number.
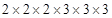
Here all factors are in groups of 3’s (in triplets)
Therefore, 216 is a perfect cube number.
(ii) 128
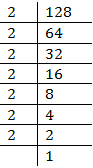
Prime factors of 128 =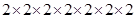 
Here one factor 2 does not appear in a 3’s group.
Therefore, 128 is not a perfect cube.
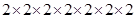
Here one factor 2 does not appear in a 3’s group.
Therefore, 128 is not a perfect cube.
(iii) 1000
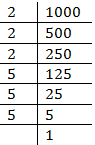
Prime factors of 1000 = 2X2X2X5X5X5
Here all factors appear in 3’s group.
Therefore, 1000 is a perfect cube.
Here all factors appear in 3’s group.
Therefore, 1000 is a perfect cube.
(iv) 100
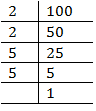
Prime factors of 100 = 2 x 2 x 5 x 5
Here all factors do not appear in 3’s group.
Therefore, 100 is not a perfect cube.
Here all factors do not appear in 3’s group.
Therefore, 100 is not a perfect cube.
(v) 46656
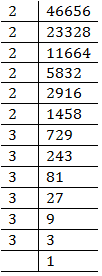
Prime factors of 46656 =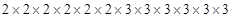 
Here all factors appear in 3’s group.
Therefore, 46656 is a perfect cube.
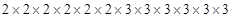
Here all factors appear in 3’s group.
Therefore, 46656 is a perfect cube.
2. Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube:
(i) 243 (ii) 256 (iii) 72 (iv) 675 (v) 100
Ans. (i) 243
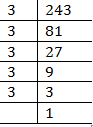
Prime factors of 243 =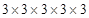 
Here 3 does not appear in 3’s group.
Therefore, 243 must be multiplied by 3 to make it a perfect cube.
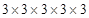
Here 3 does not appear in 3’s group.
Therefore, 243 must be multiplied by 3 to make it a perfect cube.
(ii) 256
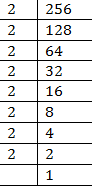
Prime factors of 256 =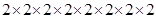 
Here one factor 2 is required to make a 3’s group.
Therefore, 256 must be multiplied by 2 to make it a perfect cube.
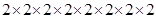
Here one factor 2 is required to make a 3’s group.
Therefore, 256 must be multiplied by 2 to make it a perfect cube.
(iii) 72
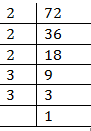
Prime factors of 72 =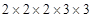 
Here 3 does not appear in 3’s group.
Therefore, 72 must be multiplied by 3 to make it a perfect cube.
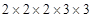
Here 3 does not appear in 3’s group.
Therefore, 72 must be multiplied by 3 to make it a perfect cube.
(iv) 675
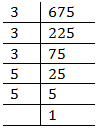
Prime factors of 675 =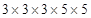 
Here factor 5 does not appear in 3’s group.
Therefore 675 must be multiplied by 5 to make it a perfect cube.
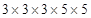
Here factor 5 does not appear in 3’s group.
Therefore 675 must be multiplied by 5 to make it a perfect cube.
(v) 100
Prime factors of 100 =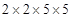 
Here factor 2 and 5 both do not appear in 3’s group.
Therefore 100 must be multiplied by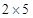
= 10 to make it a perfect cube.
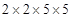
Here factor 2 and 5 both do not appear in 3’s group.
Therefore 100 must be multiplied by
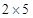= 10 to make it a perfect cube.
3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube:
(i) 81 (ii) 128 (iii) 135 (iv) 192 (v) 704
Ans. (i) 81
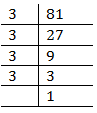
Prime factors of 81 =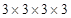 
Here one factor 3 is not grouped in triplets.
Therefore 81 must be divided by 3 to make it a perfect cube.
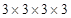
Here one factor 3 is not grouped in triplets.
Therefore 81 must be divided by 3 to make it a perfect cube.
(ii) 128
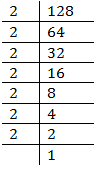
Prime factors of 128 =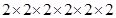 
X 2
Here one factor 2 does not appear in a 3’s group.
Therefore, 128 must be divided by 2 to make it a perfect cube.
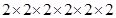X 2Here one factor 2 does not appear in a 3’s group.
Therefore, 128 must be divided by 2 to make it a perfect cube.
(iii) 135
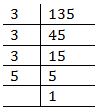
Prime factors of 135 =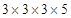 
Here one factor 5 does not appear in a triplet.
Therefore, 135 must be divided by 5 to make it a perfect cube.
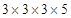
Here one factor 5 does not appear in a triplet.
Therefore, 135 must be divided by 5 to make it a perfect cube.
(iv) 192
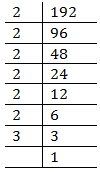
Prime factors of 192 = 2X2X2X2X2X2X3
Here one factor 3 does not appear in a triplet.
Therefore, 192 must be divided by 3 to make it a perfect cube.
Here one factor 3 does not appear in a triplet.
Therefore, 192 must be divided by 3 to make it a perfect cube.
(v) 704
Prime factors of 704 = 2X2X2X2X2X2X11
Here one factor 11 does not appear in a triplet.
Therefore, 704 must be divided by 11 to make it a perfect cube.
Here one factor 11 does not appear in a triplet.
Therefore, 704 must be divided by 11 to make it a perfect cube.
4. Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Ans. Given numbers =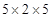 
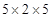
Since, Factors of 5 and 2 both are not in group of three.
Therefore, the number must be multiplied by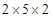
= 20 to make it a perfect cube.
Hence he needs 20 cuboids.
Therefore, the number must be multiplied by
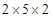= 20 to make it a perfect cube.Hence he needs 20 cuboids.
