Congruence of Triangles - Worksheets

CBSE Worksheet-1
CLASS –VII Mathematics (Congruence of Triangles)
Choose correct option in questions 1 to 4.
  1. ΔABC and ΔPQR are congruent under the correspondence ABC ↔ RQP
    Write the parts of ΔABC that correspond to RQ.
    a. AB
    b. BC
    c. AC
    d. none of these
  2. Which angle is included between the sides DE and EF of ΔDEF?
    a. ∠D
    b. ∠E
    c. ∠F
    d. none of these
  3. By applying SAS congruence rule, you want to establish that ΔPQR ≅ ΔFED. It is given that PQ = FE and RP = DF. What additional information is needed to establish the congruence?
    a. ∠P = ∠D
    b. ∠Q = ∠D
    c. ∠P = ∠F
    d. ∠R = ∠F
  4. Which congruence criterion do you use in the following?
    Given: AC = DF, AB = DE, BC = EF. So, ΔABC ≅ ΔDEF
    a. ASA rule
    b. SAS rule
    c. RHS rule
    d. SSS rule
Fill in the blanks:
  1. If two-line segments have the ____________ length, they are congruent.
  2. If two triangles are congruent, then their ____________ parts (i.e., angles and sides) that match one another are equal.
  3. In an isosceles triangle base angles opposite to the equal sides are __________.
  4. The side opposite to the right angle is called the _________ of the right-angled triangle.
  5. In triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the two triangles are congruent or not. If yes, write the congruence relation in symbolic form.
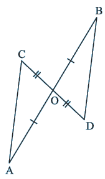
  6. In the following figure, AB and CD bisect each other at O. State the three pairs of equal parts in two triangles AOC and BOD.
CBSE Worksheet-1
CLASS –VII Mathematics (Congruence of Triangles)
Answer key
  1. c
    Explanation: Since ABC ↔RQP is the correspondence of triangles ΔABC and ΔPQR,
    We can say that AB ↔RQ
  2. b
    Explanation: The vertex common to the sides DE and EF is E. Hence the included angle is ∠E.
  3. c
    Explanation: By SAS congruence rule, two triangles are congruent if two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle.
    Here Given that PQ = FE and RP = DF, the angle included these two sides are ∠P and ∠F.
    Hence ∠P = ∠F.
  4. d
    Explanation: Since the three sides of the one triangle is equal to the corresponding sides of the other triangle, as per the SSS congruence criterion is used here.
  5. equal
  6. corresponding
  7. equal
  8. hypotenuse
  9. Yes ΔABC ≅ ΔRPQ by SSS Congruency
    Explanation: The sides of the triangle ABC are AB, BC, AC and that of triangle PQR are PQ, QR, PR
    Given that, AB = PR = RP = 3.5cm
    BC = PQ = 7.1cm
    AC = RQ = 5cm
    Hence by SSS congruency rule, since the three sides are equal the triangles ABC and RPQ are congruent
    ΔABC ≅ ΔRPQ.
  10. AO = BO, OC = OD and ∠AOC =∠BOD (vertically opposite angle)
    Explanation:

    Since AB and CD bisect each other at O, AO = BO and OC = OD. Since ∠ AOC and ∠ BOD are vertically opposite angles formed by the intersection of the line segments AB and CD,
    ∠AOC = ∠BOD
    Hence equal parts of the two triangles AOC and BOD are
    AO = BO, OC = OD and ∠AOC =∠BOD.