Congruence of Triangles - Solutions 2
CBSE Class –VII Mathematics
NCERT Solutions
Chapter 7 Congruence of Triangles (Ex. 7.2)
NCERT Solutions
Chapter 7 Congruence of Triangles (Ex. 7.2)
Question 1. Which congruence criterion do you use in the following?
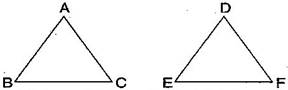
(a) Given: AC = DF, AB = DE, BC = EF
So ABC DEF
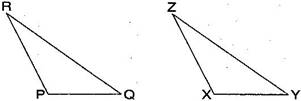
(b) Given: RP = ZX, RQ = ZY, PRQ = XZY

(b) Given: RP = ZX, RQ = ZY, PRQ = XZY
So PQR XYZ
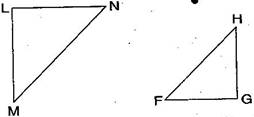
(c) Given: MLN = FGH, NML = HFG, ML = FG

(c) Given: MLN = FGH, NML = HFG, ML = FG
So LMN GFH
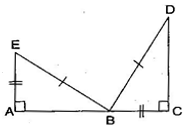
(d) Given: EB = BD, AE = CB, A = C =

(d) Given: EB = BD, AE = CB, A = C =
So ABE CDB

Answer: (a) By SSS congruence criterion, since it is given that AC = DF, AB = DE, BC = EF
The three sides of one triangle are equal to the three corresponding sides of another triangle.
Therefore, ABC DEF
(b) By SAS congruence criterion, since it is given that RP = ZX, RQ = ZY and PRQ = XZY
The two sides and one angle in one of the triangle are equal to the corresponding sides and the angle of other triangle.
Therefore, PQR XYZ
(c) By ASA congruence criterion, since it is given that MLN = FGH, NML = HFG, ML = FG.
The two angles and one side in one of the triangle are equal to the corresponding angles and side of other triangle.
Therefore, LMN GFH
(d) By RHS congruence criterion, since it is given that EB = BD, AE = CB, A = C =
Hypotenuse and one side of a right angled triangle are respectively equal to the hypotenuse and one side of another right angled triangle.
Therefore, ABE CDB
Question 2. You want to show that ART PEN:
If you have to use SSS criterion, then you need to show:
(i) AR = (ii) RT = (iii) AT =
If it is given that T = N and you are to use SAS criterion, you need to have:
(i) RT = and(ii) PN =
If it is given that AT = PN and you are to use ASA criterion, you need to have:
(i) ? (ii) ?
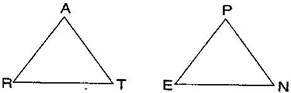

Answer: (a) Using SSS criterion, ART PEN
(i) AR = PE (ii) RT = EN (iii) AT = PN
(b) Given: T = N
Using SAS criterion, ART PEN
(i) RT = EN (ii) PN = AT
(c) Given: AT = PN
Using ASA criterion, ART PEN
(i) RAT = EPN (ii) RTA = ENP
Question 3. You have to show that AMP AMQ. In the following proof, supply the missing reasons:
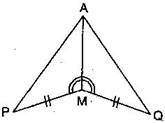

Steps
|
Reasons
|
|
|
Answer:
Steps
|
Reasons
|
|
|
Question 4. In ABC, A = B = and C =
In PQR, P = Q = and R = .
A student says that ABC PQR by AAA congruence criterion. Is he justified? Why or why not?
Answer: No, because the two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of the other.
Question 5. In the figure, the two triangles are congruent. The corresponding parts are marked. We can write RAT ?
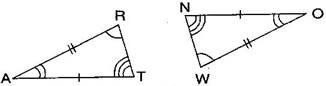

Answer: In the figure, given two triangles are congruent. So, the corresponding parts are:
A O, R W, T N.
We can write, RAT WON [By SAS congruence rule]
Question 6. Complete the congruence statement:
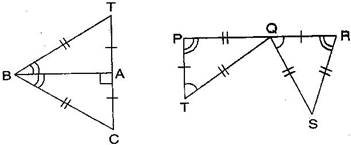

BCA ? QRS ?
Answer: In BAT and BAC, given triangles are congruent so the corresponding parts are:
B B, A A, T C
Thus, BCA BTA [By SSS congruence rule]
In QRS and TPQ, given triangles are congruent so the corresponding parts are:
P R, T Q, Q S
Thus, QRS TPQ [By SSS congruence rule]
Question 7. In a squared sheet, draw two triangles of equal area such that:
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Answer: In a squared sheet, draw ABC and PQR.
When two triangles have equal areas and
(i) these triangles are congruent, i.e., ABC PQR
[By SSS congruence rule]
Then, their perimeters are same because length of sides of first triangle are equal to the length of sides of another triangle by SSS congruence rule.
(ii) But, if the triangles are not congruent, then their perimeters are not same because lengths of sides of first triangle are not equal to the length of corresponding sides of another triangle.
Question 8. Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Answer: Let us draw two triangles PQR and ABC.
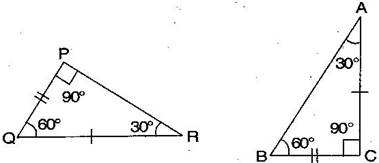
All angles are equal, two sides are equal except one side. Hence, PQR are not congruent to ABC.

All angles are equal, two sides are equal except one side. Hence, PQR are not congruent to ABC.
Question 9. If ABC and PQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
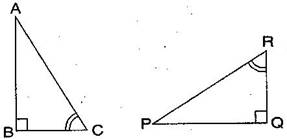
Answer: ABC and PQR are congruent. Then one additional pair is =

Answer: ABC and PQR are congruent. Then one additional pair is =
Given: B = Q =
C = R
=
Therefore, ABC PQR [By ASA congruence rule]
Question 10. Explain, why ABC FED.
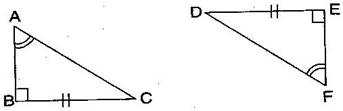

Answer: Given: A = F, BC = ED, B = E
In ABC and FED,
B = E =
A = F
BC = ED
Therefore, ABC FED [By RHS congruence rule]
