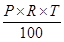Comparing Quantities - Revision Notes
CBSE Class–VII Subject Mathematics
Revision Notes
Chapter – 8
Comparing Quantities
Revision Notes
Chapter – 8
Comparing Quantities
Comparing Quantities: We are often required to compare two quantities, in our daily life. They may be heights, weights, salaries, marks etc. To compare two quantities, their units must be the same.- We are often required to compare two quantities in our daily life. They may be heights, weights, salaries, marks etc.
- While comparing heights of two persons with heights150 cm and 75 cm, we write it as the ratio 150 : 75 or 2 : 1.
- Ratio: A ratio compares two quantities using a particular operation.
- Percentage: Percentage are numerators of fractions with denominator 100. Percent is represent by the symbol % and means hundredth too.
- Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say the two given ratios are equivalent.
- If two ratios are equivalent then the four quantities are said to be in proportion. For example, the ratios 8 : 2 and 16 : 4 are equivalent therefore 8, 2, 16 and 4 are in proportion.
- A way of comparing quantities is percentage. Percentages are numerators of fractions with denominator 100. Per cent means per hundred. For example 82% marks means 82 marks out of hundred.
- Fractions can be converted to percentages and vice-versa. For example,
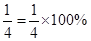 whereas,
whereas, 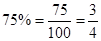
- Decimals too can be converted to percentages and vice-versa. For example,
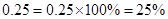
- Percentages are widely used in our daily life,
(a) We have learnt to find exact number when a certain per cent of the total quantity is given.
(b) When parts of a quantity are given to us as ratios, we have seen how to convert them to percentages.
(c) The increase or decrease in a certain quantity can also be expressed as percentage.
(d) The profit or loss incurred in a certain transaction can be expressed in terms of percentages.
(e) While computing interest on an amount borrowed, the rate of interest is given in terms of per cents. For example, ` 800 borrowed for 3 years at 12% per annum. - Simple Interest: Principal means the borrowed money.
- The extra money paid by borrower for using borrowed money for given time is called interest (I).
- The period for which the money is borrowed is called ‘Time Period’ (T).
- Rate of interest is generally given in percent per year.
- Interest (I):