Algebraic Expressions - Solutions 1
CBSE Class –VII Mathematics
NCERT Solutions
Algebraic Expressions (Ex. 12.1)
NCERT Solutions
Algebraic Expressions (Ex. 12.1)
Question 1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations:
- Subtraction of {tex}z{/tex} from {tex}y.{/tex}
- One-half of the sum of numbers {tex}x{/tex} and {tex}y.{/tex}
- The number {tex}z{/tex} multiplied by itself.
- One-fourth of the product of numbers {tex}p{/tex} and {tex}q.{/tex}
- Numbers {tex}x{/tex} and {tex}y{/tex} both squared and added.
- Number 5 added to three times the product of {tex}m{/tex} and {tex}n.{/tex}
- Product of numbers {tex}y{/tex} and {tex}z{/tex} subtracted from 10.
- Sum of numbers {tex}a{/tex} and {tex}b{/tex} subtracted from their product.
Answer: (i) {tex}y - z{/tex}
(ii) {tex}\frac{{x + y}}{2}{/tex}
(iii) {tex}{z^2}{/tex}
(iv) {tex}\frac{{pq}}{4}{/tex}
(v) {tex}{x^2} + {y^2}{/tex}
(vi) {tex}3mn + 5{/tex}
(vii) {tex}10 - yz{/tex}
(viii) {tex}ab - \left( {a + b} \right){/tex}
Question 2.(i) Identify the terms and their factors in the following expressions, show the terms and factors by tree diagram:
(a) {tex}x - 3{/tex}
(b) {tex}1 + x + {x^2}{/tex}
(c) {tex}y - {y^3}{/tex}
(d) {tex}5x{y^2} + 7{x^2}y{/tex}
(e) {tex} - ab + 2{b^2} - 3{a^2}{/tex}
(ii) Identify the terms and factors in the expressions given below:
(a) {tex} - 4x + 5{/tex}
(b) {tex} - 4x + 5y{/tex}
(c) {tex}5y + 3{y^2}{/tex}
(d) {tex}xy + 2{x^2}{y^2}{/tex}
(e) {tex}pq + q{/tex}
(f) {tex}1.2ab - 2.4b + 3.6a{/tex}
(g) {tex}\frac{3}{4}x + \frac{1}{4}{/tex}
(h) {tex}0.1{p^2} + 0.2{q^2}{/tex}
Answer: (i) (a) {tex}x - 3{/tex}
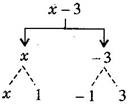
(b) {tex}1 + x + {x^2}{/tex}
Expression
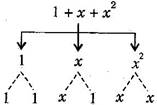
(c) {tex}y - {y^3}{/tex}
Expression
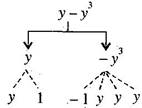
(d) {tex}5x{y^2} + 7{x^2}y{/tex}
Expression
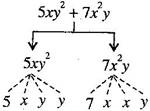
(e) {tex} - ab + 2{b^2} - 3{a^2}{/tex}
Expression
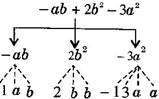
(ii) (a) {tex} - 4x + 5{/tex}
Terms: {tex} - 4x,5{/tex}
Factors: {tex} - 4,x{\text{ }};{\text{ }}5{/tex}
(b) {tex} - 4x + 5y{/tex}
Terms: {tex} - 4x,5y{/tex}
Factors: {tex} - 4,x{\text{ }};{\text{ }}5,y{/tex}
(c) {tex}5y + 3{y^2}{/tex}
Terms: {tex}5y,3{y^2}{/tex}
Factors: {tex}5,y{\text{ }};{\text{ }}3,y,y{/tex}
(d) {tex}xy + 2{x^2}{y^2}{/tex}
Terms: {tex}xy,2{x^2}{y^2}{/tex}
Factors: {tex}x,y{\text{ }};{\text{ }}2x,x,y,y{/tex}
(e) {tex}pq + q{/tex}
Terms: {tex}pq,q{/tex}
Factors: {tex}p,q{\text{ }};{\text{ }}q{/tex}
(f) {tex}1.2ab - 2.4b + 3.6a{/tex}
Terms: {tex}1.2ab, - 2.4b,3.6a{/tex}
Factors: {tex}1.2,a,b{\text{ }};{\text{ }} - 2.4,b{\text{ }};{\text{ }}3.6,a{/tex}
(g) {tex}\frac{3}{4}x + \frac{1}{4}{/tex}
Terms: {tex}\frac{3}{4}x,\frac{1}{4}{/tex}
Factors: {tex}\frac{3}{4},x{\text{ }};{\text{ }}\frac{1}{4}{/tex}
(h) {tex}0.1{p^2} + 0.2{q^2}{/tex}
Terms: {tex}0.1{p^2},0.2{q^2}{/tex}
Factors: {tex}0.1,p,p{\text{ }};{\text{ }}0.2,q,q{/tex}
Question 3.Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i){tex}5 - 3{t^2}{/tex}
(ii){tex}1 + t + {t^2} + {t^3}{/tex}
(iii){tex}x + 2xy + 3y{/tex}
(iv) {tex}100m + 1000n{/tex}
(v){tex} - {p^2}{q^2} + 7pq{/tex}
(vi) {tex}1.2a + 0.8b{/tex}
(vii) {tex}3.14{r^2}{/tex}
(viii) {tex}2\left( {l + b} \right){/tex}
(ix) {tex}0.1y + 0.01{y^2}{/tex}
Answer:
| S.No. | Expression | Terms | Numerical Coefficient |
| (i) | {tex}5 - 3{t^2}{/tex} | {tex} - 3{t^2}{/tex} | {tex} - 3{/tex} |
| (ii) | {tex}1 + t + {t^2} + {t^3}{/tex} | {tex}t{/tex} | 1 |
| {tex}{t^2}{/tex} | 1 | ||
| {tex}{t^3}{/tex} | 1 | ||
| (iii) | {tex}x + 2xy + 3y{/tex} | {tex}x{/tex} | 1 |
| {tex}2xy{/tex} | 2 | ||
| {tex}3y{/tex} | 3 | ||
| (iv) | {tex}100m + 1000n{/tex} | {tex}100m{/tex} | 100 |
| {tex}1000n{/tex} | 1000 | ||
| (v) | {tex} - {p^2}{q^2} + 7pq{/tex} | {tex} - {p^2}{q^2}{/tex} | {tex} - 1{/tex} |
| {tex}7pq{/tex} | 7 | ||
| (vi) | {tex}1.2a + 0.8b{/tex} | {tex}1.2a{/tex} | 1.2 |
| {tex}0.8b{/tex} | 0.8 | ||
| (vii) | {tex}3.14{r^2}{/tex} | {tex}3.14{r^2}{/tex} | 3.14 |
| (viii) | {tex}2\left( {l + b} \right) = 2l + 2b{/tex} | {tex}2l{/tex} | 2 |
| {tex}2b{/tex} | 2 | ||
| (ix) | {tex}0.1y + 0.01{y^2}{/tex} | {tex}0.1y{/tex} | 0.1 |
| {tex}0.01{y^2}{/tex} | 0.01 |
Question 4.(a) Identify terms which contain {tex}x{/tex} and give the coefficient of {tex}x.{/tex}
(i) {tex}{y^2}x + y{/tex}
(ii) {tex}13{y^2} - 8yx{/tex}
(iii) {tex}x + y + 2{/tex}
(iv) {tex}5 + z + zx{/tex}
(v) {tex}1 + x + xy{/tex}
(vi) {tex}12x{y^2} + 25{/tex}
(vii) {tex}7x + x{y^2}{/tex}
(b) Identify terms which contain {tex}{y^2}{/tex} and give the coefficient of {tex}{y^2}.{/tex}
(i) {tex}8 - x{y^2}{/tex}
(ii) {tex}5{y^2} + 7x{/tex}
(iii) {tex}2{x^2}y - 15x{y^2} + 7{y^2}{/tex}
Answer: (a)
| S.No. | Expression | Term with factor {tex}x{/tex} | Coefficient of {tex}x{/tex} |
| (i) | {tex}{y^2}x + y{/tex} | {tex}{y^2}x{/tex} | {tex}{y^2}{/tex} |
| (ii) | {tex}13{y^2} - 8yx{/tex} | {tex} - 8yx{/tex} | {tex} - 8y{/tex} |
| (iii) | {tex}x + y + 2{/tex} | {tex}x{/tex} | 1 |
| (iv) | {tex}5 + z + zx{/tex} | {tex}zx{/tex} | {tex}z{/tex} |
| (v) | {tex}1 + x + xy{/tex} | {tex}x{/tex} | 1 |
| {tex}xy{/tex} | {tex}y{/tex} | ||
| (vi) | {tex}12x{y^2} + 25{/tex} | {tex}12x{y^2}{/tex} | {tex}12{y^2}{/tex} |
| (vii) | {tex}7x + x{y^2}{/tex} | {tex}x{y^2}{/tex} | {tex}{y^2}{/tex} |
| {tex}7x{/tex} | 7 |
(b)
| S.No. | Expression | Term contains {tex}{y^2}{/tex} | Coefficient of {tex}{y^2}{/tex} |
| (i) | {tex}8 - x{y^2}{/tex} | {tex} - x{y^2}{/tex} | {tex} - x{/tex} |
| (ii) | {tex}5{y^2} + 7x{/tex} | {tex}5{y^2}{/tex} | 5 |
| (iii) | {tex}2{x^2}y - 15x{y^2} + 7{y^2}{/tex} | {tex} - 15x{y^2}{/tex} | {tex} - 15x{/tex} |
| {tex}7{y^2}{/tex} | 7 |
Question 5.Classify into monomials, binomials and trinomials:
(i) {tex}4y - 7x{/tex}
(ii) {tex}{y^2}{/tex}
(iii) {tex}x + y - xy{/tex}
(iv) {tex}100{/tex}
(v) {tex}ab - a - b{/tex}
(vi) {tex}5 - 3t{/tex}
(vii) {tex}4{p^2}q - 4p{q^2}{/tex}
(viii) {tex}7mn{/tex}
(ix) {tex}{z^2} - 3z + 8{/tex}
(x) {tex}{a^2} + {b^2}{/tex}
(xi) {tex}{z^2} + z{/tex}
(xii) {tex}1 + x + {x^2}{/tex}
Answer:
| S.No. | Expression | Type of Polynomial |
| (i) | {tex}4y - 7z{/tex} | Binomial |
| (ii) | {tex}{y^2}{/tex} | Monomial |
| (iii) | {tex}x + y - xy{/tex} | Trinomial |
| (iv) | 100 | Monomial |
| (v) | {tex}ab - a - b{/tex} | Trinomial |
| (vi) | {tex}5 - 3t{/tex} | Binomial |
| (vii) | {tex}4{p^2}q - 4p{q^2}{/tex} | Binomial |
| (viii) | {tex}7mn{/tex} | Monomial |
| (ix) | {tex}{z^2} - 3z + 8{/tex} | Trinomial |
| (x) | {tex}{a^2} + {b^2}{/tex} | Binomial |
| (xi) | {tex}{z^2} + z{/tex} | Binomial |
| (xii) | {tex}1 + x + {x^2}{/tex} | Trinomial |
Question 6. State whether a given pair of terms is of like or unlike terms:
(i) {tex}1,{\text{ }}100{/tex}
(ii) {tex} - 7x,\frac{5}{2}x{/tex}
(iii) {tex} - 29x, - 29y{/tex}
(iv) {tex}14xy,42yx{/tex}
(v) {tex}4{m^2}p,4m{p^2}{/tex}
(vi) {tex}12xz,12{x^2}{z^2}{/tex}
(ii) {tex} - 7x,\frac{5}{2}x{/tex}
(iii) {tex} - 29x, - 29y{/tex}
(iv) {tex}14xy,42yx{/tex}
(v) {tex}4{m^2}p,4m{p^2}{/tex}
(vi) {tex}12xz,12{x^2}{z^2}{/tex}
Answer:
| S.No. | Pair of terms | Like / Unlike terms |
| (i) | 1, 100 | Like terms |
| (ii) | {tex} - 7x,\frac{5}{2}x{/tex} | Like terms |
| (iii) | {tex} - 29x, - 29y{/tex} | Unlike terms |
| (iv) | {tex}14xy,42yx{/tex} | Like terms |
| (v) | {tex}4{m^2}p,4m{p^2}{/tex} | Unlike terms |
| (vi) | {tex}12xz,12{x^2}{z^2}{/tex} | Unlike terms |
Question 7.Identify like terms in the following:
(a) - xy2, -4yx2, 8x2, 2xy2, 7y, -11x2 -100x, -11yx, 20x2y, - 6x2, y, 2xy, 3x
(b) 10pq, 7p, 8q, -p2q2, -7qp, -100q, -23, 12q2p2, -5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
(a) - xy2, -4yx2, 8x2, 2xy2, 7y, -11x2 -100x, -11yx, 20x2y, - 6x2, y, 2xy, 3x
(b) 10pq, 7p, 8q, -p2q2, -7qp, -100q, -23, 12q2p2, -5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
Answer: (a) Like terms are:
(i) {tex} - x{y^2},2x{y^2}{/tex}
(ii) {tex} - 4y{x^2},20{x^2}y{/tex}
(iii) {tex}8{x^2}, - 11{x^2}, - 6{x^2}{/tex}
(iv) {tex}7y,y{/tex}
(v) {tex} - 100x,3x{/tex}
(vi) {tex} - 11yx,2xy{/tex}
(i) {tex} - x{y^2},2x{y^2}{/tex}
(ii) {tex} - 4y{x^2},20{x^2}y{/tex}
(iii) {tex}8{x^2}, - 11{x^2}, - 6{x^2}{/tex}
(iv) {tex}7y,y{/tex}
(v) {tex} - 100x,3x{/tex}
(vi) {tex} - 11yx,2xy{/tex}
(b) Like terms are:
(i) {tex}10pq, - 7pq,78pq{/tex}
(ii) {tex}7p,2405p{/tex}
(iii) {tex}8q, - 100q{/tex}
(iv) {tex} - {p^2}{q^2},12{p^2}{q^2}{/tex}
(v) {tex} - 12,41{/tex}
(vi) {tex} - 5{p^2},701{p^2}{/tex}
(vii) {tex}13{p^2}q,q{p^2}{/tex}
(i) {tex}10pq, - 7pq,78pq{/tex}
(ii) {tex}7p,2405p{/tex}
(iii) {tex}8q, - 100q{/tex}
(iv) {tex} - {p^2}{q^2},12{p^2}{q^2}{/tex}
(v) {tex} - 12,41{/tex}
(vi) {tex} - 5{p^2},701{p^2}{/tex}
(vii) {tex}13{p^2}q,q{p^2}{/tex}
