Algebraic Expressions and Identities - Revision Notes
CBSE Class 8 Mathematics
Revision Notes
Chapter – 9
Algebraic Expressions and Identities
Revision Notes
Chapter – 9
Algebraic Expressions and Identities
- Expressions are formed from variables and constants.
- Constant: A symbol having a fixed numerical value. Example: 2, , 2.1, etc.
- Variable: A symbol which takes various numerical values. Example: x, y, z, etc.
- Algebric Expression: A combination of constants and variables connected by the sign +, -,
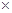 and
and 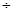 is called algebraic expression.
is called algebraic expression. - Terms are added to form expressions. Terms themselves are formed as product of factors.
- Expressions that contain exactly one, two and three terms are called monomials, binomials and trinomials respectively. In general, any expression containing one or more terms with non-zero coefficients (and with variables having non- negative exponents) is called a polynomial.
- Like terms are formed from the same variables and the powers of these variables are the same, too. Coefficients of like terms need not be the same.
- While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them; then handle the unlike terms.
- There are number of situations in which we need to multiply algebraic expressions: for example, in finding area of a rectangle, the sides of which are given as expressions.
- Monomial: An expression containing only one term. Example: -3, 4x, 3xy, etc.
- Binomial: An expression containing two terms. Example: 2x-3, 4x+3y, xy-4, etc.
- Trinomial: An expression containing three terms. Example:
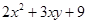 , 3x+2y+5z, etc.
, 3x+2y+5z, etc. - Polynomial: In general, any expression containing one or more terms with non-zero coefficients (and with variables having non-negative exponents). A polynomial may contain any number of terms, one or more than one.
- A monomial multiplied by a monomial always gives a monomial.
- While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the monomial.
- In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e., every term of the polynomial is multiplied by every term in the binomial (or trinomial). Note that in such multiplication, we may get terms in the product which are like and have to be combined.
- An identity is an equality, which is true for all values of the variables in the equality. On the other hand, an equation is true only for certain values of its variables. An equation is not an identity.
- The following are the standard identities:
(a + b)2 = a2 + 2ab + b2 (I)
(a – b)2 = a2 – 2ab + b2 (II)
(a + b)(a – b) = a2 – b2 (III)
Another useful identity is (x + a) (x + b) = x2 + (a + b) x + ab (IV) - The above four identities are useful in carrying out squares and products of algebraic expressions. They also allow easy alternative methods to calculate products of numbers and so on.
- Coefficients: In the term of an expression any of the factors with the sign of the term is called the coefficient of the product of the other factors.
- Terms: Various parts of an algebraic expression which are separated by + and – signs. Example: The expression 4x + 5 has two terms 4x and 5.
(i) Constant Term: A term of expression having no lateral factor.
(ii) Like term: The term having the same literal factors. Example 2xy and -4xy are like terms.
(iii) Unlike term: The terms having different literal factors. Example: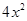 and 3xy are unlike terms.
and 3xy are unlike terms. - Factors: Each term in an algebraic expression is a product of one or more number (s) and/or literals. These number (s) and/or literal (s) are known as the factor of that term. A constant factor is called numerical factor, while a variable factor is known as a literal factor. The term 4x is the product of its factors 4 and x.
