Algebra-Solutions Ex-11.1

CBSE Class –VI Mathematics
NCERT Solutions
Chaper 11 Algebra (Ex. 11.1)

---

Question 1. Find the rule, which gives the number of matchsticks required to make the following matchsticks patterns. Use a variable to write the rule.

(a) A pattern of letter T as

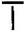
(b) A pattern of letter Z as

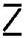
(c) A pattern of letter U as

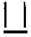
(d) A pattern of letter V as

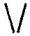
(e) A pattern of letter E as

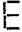
(f) A pattern of letter S as

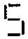
(g) A pattern of letter A as

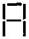
Answer: (a) Pattern of letter

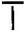
= 2n$2n$ (as two matchsticks used in each letter)

(b) Pattern of letter

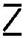
= 3n$3n$ (as three matchsticks used in each letter)

(c) Pattern of letter

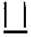
= 3n$3n$ (as three matchsticks used in each letter)

(d) Pattern of letter

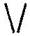
= 2n$2n$ (as two matchsticks used in each letter)

(e) Pattern of letter

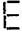
= 5n$5n$ (as five matchsticks used in each letter)

(f) Pattern of letter

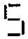
= 5n$5n$ (as five matchsticks used in each letter)

(g) Pattern of letter

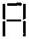
= 6n$6n$ (as six matchsticks used in each letter)

Question 2. We already know the rule for the pattern of letter L, C and F. Some of the letters from Q.1 (given above) give us the same rule as that given by L. Which are these? Why does this happen?

Answer: The letter ‘T’ and ‘V’ that has pattern 2n,$2n,$ since 2 matchsticks are used in all these letters.

Question 3. Cadets are marching in a parade. There are 5 cadets in a row. What is the rule, which gives the number of cadets, given the number of rows? (Use n$n$ for the number of rows)

Answer: Number of rows = n$n$

Cadets in each row = 5
Therefore, total number of cadets = 5n$5n$

Question 4. If there are 50 mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? (Use b$b$ for the number of boxes)

Answer: Number of boxes = b$b$

Number of mangoes in each box = 50
Therefore, total number of mangoes = 50b$50b$

Question 5. The teacher distributes 5 pencils per student. Can you tell how many pencils are needed, given the number of students? (Use s$s$ for the number of students)

Answer:Number of students = s$s$

Number of pencils to each student = 5
Therefore, total number of pencils needed are = 5s$5s$

Question 6. A bird flies 1 kilometer in one minute. Can you express the distance covered by the bird in terms of its flying time in minutes? (Use t$t$ for flying time in minutes)

Answer: Time taken by bird = t$t$ minutes
Speed of bird = 1 km per minute
Therefore, Distance covered by bird = speed x time = 1×t=t$1\times t=t$ km

Question 7. Radha is drawing a dot Rangoli (a beautiful pattern of lines joining dots with chalk powder as in figure). She has 8 dots in a row. How many dots will her Rangoli have for r$r$ rows? How many dots are there if there are 8 rows? If there are 10 rows?

Answer: Number of dots in each row = 8 dots

Number of rows = r$r$
Therefore, total number of dots in r rows = 8r$8r$
When there are 8 rows, then number of dots = 8 x 8 = 64 dots
When there are 10 rows, then number of dots = 8 x 10 = 80 dots

Question 8. Leela is Radha’s younger sister. Leela is 4 years younger than Radha. Can you write Leela’s age in terms of Radha’s age? Take Radha’s age to be x$x$ years.

Answer: Radha’s age = x$x$ years

Therefore, Leela’s age = (x−4)$\left(x-4\right)$ years

Question 9. Mother has made laddus. She gives some laddus to guests and family members; still 5 laddus remain. If the number of laddus mother gave away is l,$l,$ how many laddus did she make?

Answer: Number of laddus gave away = l$l$

Number of laddus remaining = 5
Total number of laddus she make = (l+5)$\left(l+5\right)$

Question 10. Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x,$x,$ what is the number of oranges in the larger box?

Answer: Number of oranges in one box = x$x$

Number of boxes = 2
Therefore, total number of oranges in boxes = 2x$2x$

Remaining oranges = 10
Thus, number of oranges = 2x+10$2x+10$

Question 11. (a) Look at the following matchstick pattern of squares. The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint: If you remove the vertical stick at the end, you will get a pattern of Cs.)

(b) Figures below gives a matchstick pattern of triangles. As in Exercise 11 (a) above find the general rule that gives the number of matchsticks in terms of the number of triangles.

Answer:

4 matchsticks

7 matchsticks

10 matchsticks

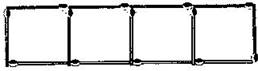
13 matchsticks

If we remove 1 from each then they makes table of 3, i.e., 3, 6, 9, 12, ……….

So the required equation = 3x+1$3x+1$ , where x$x$ is number of squares.

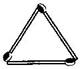
3 matchsticks

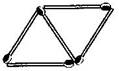
7 matchsticks

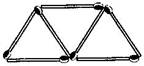
10 matchsticks

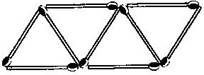
13 matchsticks

If we remove 1 from each then they makes table of 2, i.e., 2, 4, 6, 8, ……….

So the required equation = 2x+1$2x+1$ , where x$x$ is number of triangles.