प्रकाश-परावर्तन तथा अपवर्तन -
CBSE कक्षा 10 विज्ञान
पाठ-10 प्रकाश-परावर्तन तथा अपवर्तन
पुनरावृति नोट्स
पाठ-10 प्रकाश-परावर्तन तथा अपवर्तन
पुनरावृति नोट्स
'प्रकाश' एक प्रकार की उर्जा है, जो हमें वस्तुएं देखने में हमारी सहायता करता है।
इस अध्याय में हम प्रकाश का परावर्तन और प्रकाश का अपवर्तन किस प्रकार होता है, के बारे में पढ़ेंगे।
इस अध्याय में हम प्रकाश का परावर्तन और प्रकाश का अपवर्तन किस प्रकार होता है, के बारे में पढ़ेंगे।
- प्रकाश को हम एक सरल रेखीय पथ पर इंगित करते हैं जिसे प्रकाश किरण कहते हैं।
- प्रकाश का परावर्तन-
जब प्रकाश की किरणें, उच्चकोटि की पॉलिश किये हुए पृष्ठ पर पड़ती है, तो अधिकांश प्रकाश परावर्तित हो जाता है। - परावर्तन के नियम
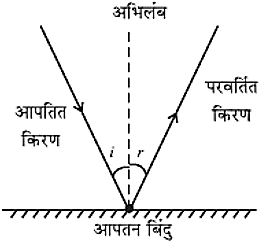
- आपतन कोण हमेशा परावर्तन कोण के बराबर होता है।
- आपतित किरण, परावर्तित किरण तथा दर्पण के आपतन बिंदु पर अभिलंब, सभी एक ही तल में होता हैं।
- समतल दर्पण द्वारा बना प्रतिबिंब-
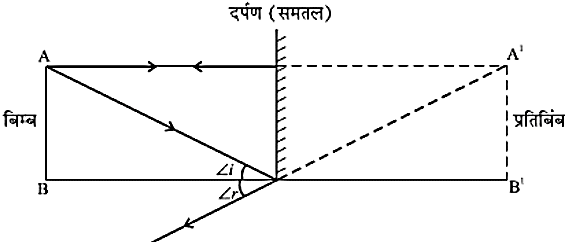
- सदैव आभासी (प्रतिबिंब जो पर्दे पर नहीं बनता) प्रतिबिंब बनता है।
- प्रतिबिंब का साइज, बिंब के साइज के बराबर होता है।
- प्रतिबिम्ब पार्श्व परिवर्तित होता है।
- प्रतिबिंब उतनी ही दूरी पर बनता, जितनी दूरी पर दर्पण के सामने बिंब रखा होता है।
- गोलीय दर्पण द्वारा परावर्तन
गोलीय दर्पण का परावर्तक पृष्ठ अंदर की ओर या बाहर की ओर वक्रित हो सकता हैं।
उदाहरण 'चम्मच' → चम्मच का गोलीय पृष्ठ को गोलीय दर्पण समझा जा सकता है।
अगर चम्मच का गोलीय पृष्ठ अंदर की ओर होता है। → तो वह अवतल दर्पण की भांति कार्य करेगी
अगर चम्मच को गोलीय पृष्ठ बाहर की ओर होता है। → तो वह उत्तल दर्पण की भांति कार्य करेगी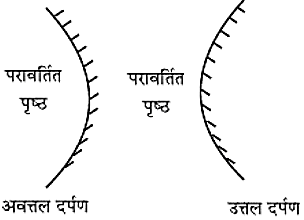
- कुछ शब्द और पद जो गोलीय दर्पण से संबंधित है।
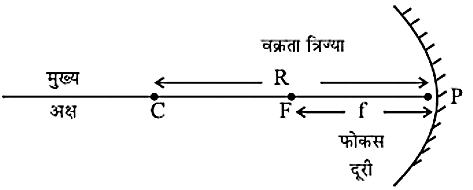
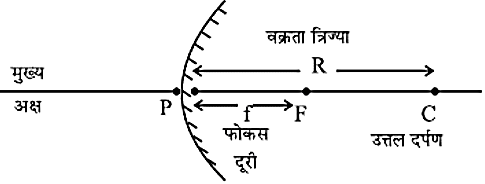
- मुख्य अक्ष- गोलीय दर्पण के ध्रुव और वक्रता त्रिज्या से गुजरने वाली सीधी रेखा को दर्पण का मुख्य अक्ष कहते हैं।
- ध्रुव- गोलीय दर्पण के परावर्तक पृष्ठ के केन्द्र को दर्पण का ध्रुव कहते हैं।
- द्धारक- गोलीय दर्पण के परावर्तक पृष्ठ की इस सीमा रेखा का व्यास दर्पण का द्धारक कहलाता है।
- वक्रता केन्द्र- गोलीय दर्पण का परावर्तक पृष्ठ एक गोले का भाग है। इस गोले के केन्द्र को दर्पण का वक्रता केन्द्र कहते हैं।
- वक़ता त्रिज्या- ध्रुव और वक्रता केन्द्र के बीच की दूरी PC = R (जिसे R से दर्शाया जाता है)
- फोकस बिंदु- अवतल दर्पण के मुख्य अक्ष के सामांतर आपतित किरणें, परावर्तित होकर मुख्य अक्ष के एक बिंदु पर मिलती है जिसे फोकस बिंदु कहते हैं।
- उत्तल दर्पण- में वे उस बिंदु से आती प्रतीत होती है।
- फोकस दूरी- गोलीय दर्पण के ध्रुव तथा मुख्य फोकस के बीच की दूरी फोकस दूरी कहलाती है। इसे f से दर्शाया जाता हैं।
फोकस दूरी तथा वक्रता त्रिज्या में संबंध
- गोलीय दर्पणों द्वारा प्रतिबिंब बनना-
कम से कम दो परावर्तित किरणों के प्रतिछेदन पर चित्र के प्रतिबिंब की स्थिति ज्ञात की जा सकती हैं।
गोलीय दर्पण द्वारा प्रतिबिंब बनाने से पहले हमें कुछ विशेष बातों का ध्यान रखना चाहिए।- दर्पण के मुख्य अक्ष के सामांतर किरण परावर्तन के पश्चात अवतल दर्पण के मुख्य फोकस से गुजरेगी।
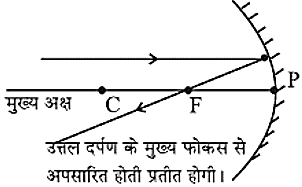
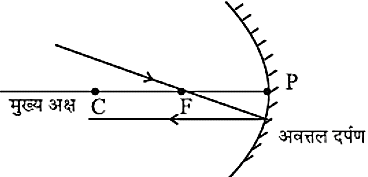
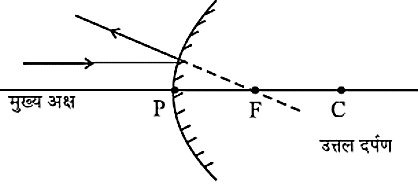
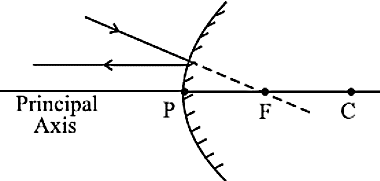
- अवतल दर्पण के वक्रता केन्द्र से गुजरने वाली किरण अथवा उत्तल दर्पण के और निर्देशित किरण, परावर्तन के पश्चात उसी पथ के अनुदिश वापस परावर्तित हो जाती है।
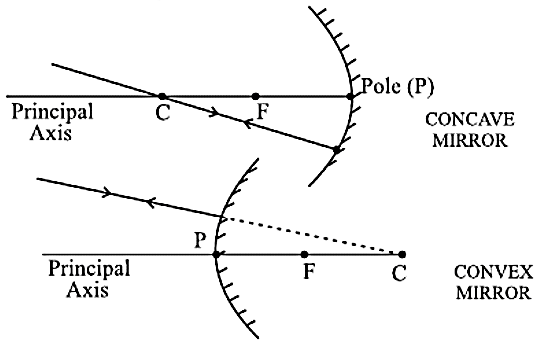
- ध्रुव पर आपतित होने वाली किरण आपतित कोण के बराबर परावर्तित कोण (ध्रुव पर) पर ही परावर्तित हो जाती है।
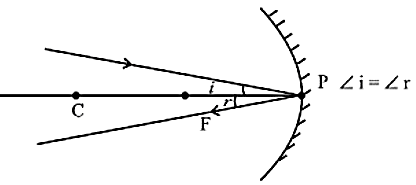
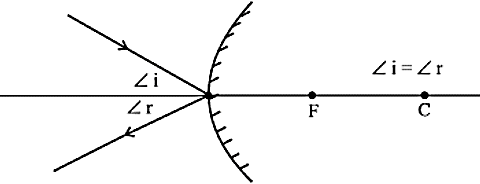
- दर्पण के मुख्य अक्ष के सामांतर किरण परावर्तन के पश्चात अवतल दर्पण के मुख्य फोकस से गुजरेगी।
- प्रकाश की किरण, जब वक्रता केन्द्र से गुजरती है तो यह आपतित किरण गोलीय दर्पण के परावर्तक पृष्ठ पर अभिलेव के अनुदिश पड़ती हैं। इस किरण के द्वारा हम आपतित कोण और परावर्तित कोण का पता लगा सकते हैं।
वक्रता केंद्र से गुजरने वाली रेखा, अपवर्तित बिन्दु पर अभिलंब बनाती है।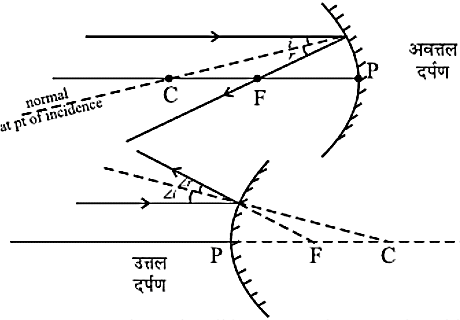
- Image formation by a concave mirror for different position of the object (अवतल दर्पण द्वारा प्रतिबिंब बनाना)
- बिंब - (अनंत पर)
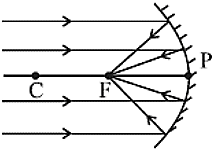
प्रतिबिंब की स्थिति At focus
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब का आकार - बहुत छोटा - बिंब - (C से परे)
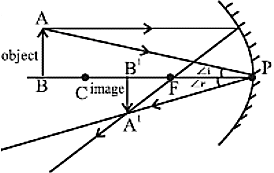
प्रतिबिंब की स्थित Between F&C
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब का आकार - छोटा - बिंब - (C पर)
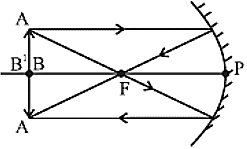
प्रतिबिंब की स्थिति - At C
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब का आकार - प्रतिबिंब के समान - बिंब - Between C & F
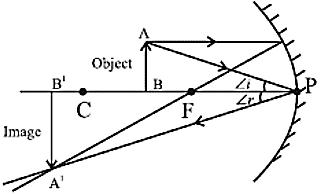
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब की स्थिति - Beyond C
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब का आकार - बड़ी - बिंब - F पर
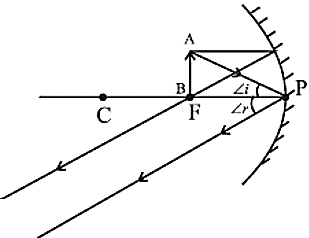
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब की स्थिति - अनंत पर
प्रकृति - वास्तविक और उल्टी
प्रतिबिंब का आकार - बहुत बड़ी - बिंब - Between F&P (Special Case)
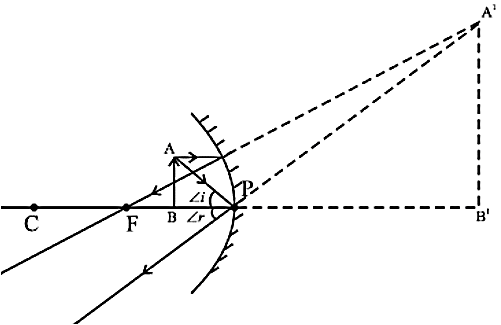
प्रकृति - आभासी और सीधी
प्रतिबिंब की स्थिति - दर्पण के पीछे
प्रतिबिंबा का आकार - बहुत बड़ी
- बिंब - (अनंत पर)
- Image formation by Convex Mirror उत्तल दर्पण द्वारा बने प्रतिबिंब
- बिंब - अनंत पर
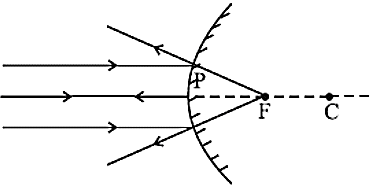
प्रतिबिंब की स्थिति - At focus
प्रतिबिंब का आकार - बहुत छोटा
प्रकृति - आभासी और सीधी - बिंब - कहीं भी पर्दण के ध्रुव और अनंत के बीच
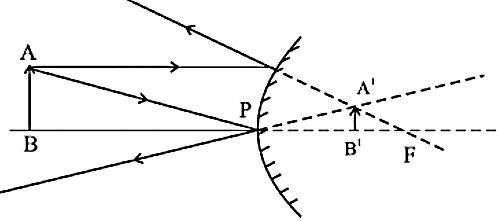
प्रतिबिंब की स्थिति - P और F के बीच में
प्रतिबिंब का आकार - छोटा
प्रकृति - आभासी तथा सीधा
- बिंब - अनंत पर
- अवतल दर्पण का उपयोग
- टॉर्च, सर्चलाइड तथा वाहनों के अग्रदीपों (Headlight) में
- चेहरे का बड़ा प्रतिबिंब देखने के लिए शेविंग दर्पणों के रूप में उपयोग
- दंत विशेषज्ञ द्वारा मरीजों के दांत देखने के लिए।
- सौर भट्टियों में सूर्य के प्रकाश को केंद्रित करने के लिए
- उत्तल दर्पण का उपयोग
सामान्यतः वाहनों के पश्च-दृश्य दर्पणों के रूप में किया जाता है। इनमें ड्राइवर अपने पीछे के वाहनों को देख सकता है। समतल दर्पण की तुलना में उत्तल दर्पण ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में समर्थ बनाते हैं। - गोलीय दर्पणों द्वारा परावर्तन के लिए चिन्ह परिपाटी-
- बिंब दर्पण के सदैव बायीं ओर रखा जाता हैं।
- मुख्य अक्ष के सामांतर दूरियां दर्पण के ध्रुव से मापी जाती है।
मूल बिंदु को हम ध्रुव (P) मानते हैं।
मूल बिंदु के दायीं ओर - (+x अक्ष) - सभी धनात्मक हैं।
मूल बिंदु के बायीं ओर -( - xअक्ष) - सभी दूरियां ऋणात्मक है।
मुख्य अक्ष के लम्बवत् ऊपर की ओर - (+ xअक्ष) - सभी दूरियां धनात्मक हैं। मुख्य अक्ष के लम्बवत् नीचे की ओर - (-y अक्ष) - सभी दूरियां ऋणात्मक हैं।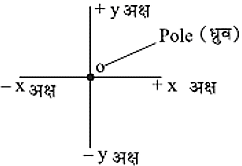
- दर्पण सूत्र
where
f ध्रुव से मुख्य फोकस की दूरी
u ध्रुव से बिंब की दूरी
v ध्रुव से प्रतिबिंब की दूरी
R ध्रुव से वक्रता केन्द्र की दूरी - आवर्धन (m)-
इसे प्रतिबिंब की ऊंचाई तथा बिंब की ऊंचाई के अनुपात के रूप में व्यक्त किया जाता है।
h1 = प्रतिबिंब की ऊंचाई
h = बिंब की ऊंचाई
आवर्धन (m) बिंब दूरी (u) तथा प्रतिबिंब दूरी (v) से भी संबंधित है।
h1 प्रतिबिंब की मुख्य अक्ष से ऊंचाई
h1 बिंब की मुख्य अक्ष की ऊंचाई
अगर
m > 1 ______ प्रतिबिंब आवर्धित हैं।
m = 1 ______ प्रतिबिंब, बिंब के समान आकार का हैं।
m < 1 ______ प्रतिबिंब, बिंब की तुलना में छोटा है।
कुछ छोटी-छोटी बातें, चिन्ह परिपाटी को याद रखने योग्य गोलीय दर्पण के लिए- बिंब की ऊंचाई (h) हमेशा धनात्मक (+ve)
- प्रतिबिंब की ऊंचाई (h) वास्तविक ऋणात्मक (–ve)
आभासी धनात्मक (+ve) - बिंब की दूरी ध्रुव से (u) हमेशा ऋणात्मक (-ve)
- प्रतिबिंब की दूरी ध्रुव से (v) वास्तविक ऋणात्मक (-ve)
आभासी धनात्मक (+ve) - फोकस दूरी ध्रुव से (f) अवतल दर्पण हमेशा ऋणात्मक (-ve)
उत्तल दर्पण हमेशा धनात्मक (-ye)
- प्रकाश का अपवर्तन
जब प्रकाश एक पारदर्शी माध्यम से दूसरे में प्रवेश करता है तो वह अपनी दिशा बदलता है। प्रकाश की चाल भी बदल जाती है।
जब प्रकार विरल से सघन माध्यम की ओर गमन करता है तो इसकी चाल घट जाती हैं।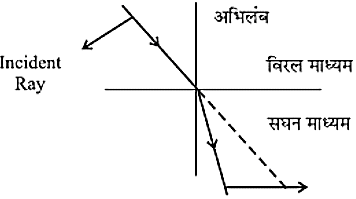
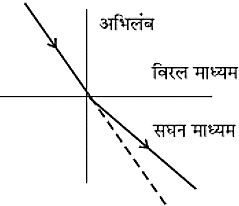
जब प्रकाश की किरण बिरल से सघन माध्यम की और चलता है तो वह अपवर्तन के पश्चात अभिलंब की ओर झुक जाता हैं। जब प्रकाश की किरण सघन से विरल माध्यम की ओर चलता है तो वह अपवर्तन के पश्चात अभिलंब से दूर मुड़ जाता है। - कुछ ऐसे अनुभव जो हम प्रकाश के अपवर्तन के कारण देखते हैं जैसे-
- टब में पानी के तल पर पड़ा पत्थर हमें थोड़ा-सा ऊपर की ओर दिखाई देता है। अर्थात् अपनी वास्तविक स्थिति से अलग।
- मछली पानी के अंदर अपने वास्तविक आकार से थोड़ी बड़ी नजर आती हैं।
- पानी में आंशिक रूप से डूबी हुई पेंसिल मुड़ी हुई प्रतीत होती है।
- कांच के आयताकार स्लेब से अपवर्तन
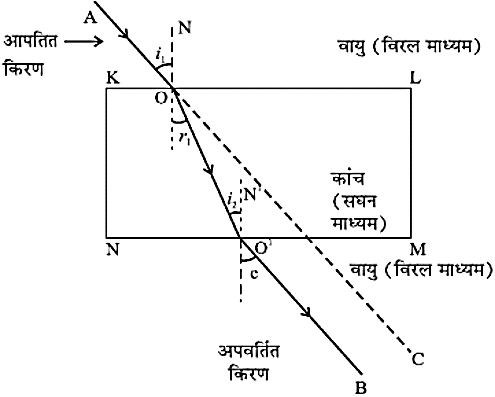
इस क्रियाकलाप में प्रकाश किरण ने अपनी दिशा आपतन बिंदुओं O और O' पर अपरिवर्तित की हैं। बिंदु O और O' दोनों पारदर्शी माध्यमों की पृथक करने वाले पृष्ठों पर स्थित है।
जब आपतित प्रकाश की किरण AO विरल माध्यम (वायु) से सघन माध्यम (कांच) में प्रवेश करती हैं। तो अभिलंब (O पर) की तरफ झुक जाती है।
बिंदु O पर जब प्रकाश की किरण सघन माध्यम (कांच) से विरल माध्यम में प्रवेश करती हैं तो अभिलंब (O' पर) से दूर मुड़ जाती है।
O'B निर्गत किरण हो और OO' अपवर्तित किरण हैं।
अगर आपतित किरण AO को C तक बढ़ाया जाया तो हम देखेंगे कि AC, निर्गत O'B के सामांतर हैं। अर्थात अपवर्तन के कारण प्रकाश की किरण में थोड़ा सा पाश्विक विस्थापन होता है। - अपवर्तन के नियम-
- आपतित किरण, अपवर्तित किरण तथा दोनों माध्यमों को पृथक करने वाले पृष्ठ के आपतन बिंदु पर अभिलंब सभी एक ही तल पर होते हैं।
- प्रकाश के किसी निश्चित रंग तथा निश्चित माध्यमों के युग्म के लिए आपतन कोण की ज्या (sine) तथा अपवर्तन कोण की ज्या (sine) का अनुपात स्थिर होता हैं। इसे स्नेल (Snell's) का अपवर्तन नियम भी कहते हैं।
- स्थिरांक- इसके मान को दूसरे माध्यम का पहले माध्यम के सापेक्ष, अपवर्तनांक कहते हैं।
n2 दूसरे माध्यक का अपवर्तनाम
n1 पहले माध्यम का अपवर्तनाक - कांच का अपवर्तनांक वायु के सापेक्ष- प्रकाश की चाल वायु में और प्रकाश की चाल कांच के अनुपात के बराबर होती हैं।
प्रकाश की चाल वायु में / प्रकाश की चाल कांच में
g = कांच (glass)
a = वायु (air)
C प्रकाश की चाल निर्वात में = 3×103 m/s
वायु में प्रकाश की चाल निर्वात की अपेक्षा थोड़ी से ही कम होती है। - वायु का अपवर्तनाक कांच के सापेक्ष
प्रकाश की चाल वायु में / प्रकाश की चाल कांच में
यदि वायु में प्रकाश की चाल (C) है और माध्यम में प्रकाश की चाल (V) है तो किसी माध्यम का अपवर्तनाक होगा।
(m माध्यम) nm = वायु में में प्रकाश की चाल / माध्यम में प्रकाश की चाल
जल का अपवर्तनांक (nw) = 1.33
कांच का अपवर्तनांक (ng) = 1.52 - गोलीय लैंस- दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम, जिसका एक या दो पृष्ठ गोलीय है। गोलीय लैंस कहलाता है।
- उत्तल लैंस- किसी लैंस में बाहर की ओर उभरे दो गोलीय पृष्ठ हो सकते हैं। ऐसे लैंस को दि-उत्तल लैंस कहते हैं या केवल उत्तल लैंस भी कह सकते हैं।
उत्तल लैंस प्रकाश की किरणों को अभिसारित करता है इसलिए इसे अभिसारी लैंस भी। कहते हैं। - अवतल लैंस- एक दि-अवतल लैंस अंदर की ओर वक्रित दो गोलीय पृष्ठों से घिरा होता हैं। यह बीच की अपेक्षा, किनारों से मोटा होता ही इसे अवतल लैंस कहते हैं।
यह प्रकाश की किरणों को अपसरित करता हैं। इसलिए इसे अपसारी लैंस भी कहते हैं। - कुछ शब्द और पद जो गोलीय लैंस से संबंधित हैं-
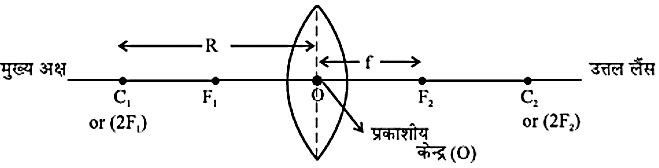
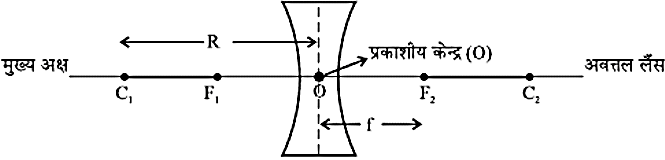
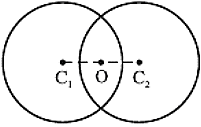
- वक्रता केन्द्र- किसी लैंस में चाहे वह उत्तल हों अथवा अवतल, दो गोलीय पृष्ठ होते हैं। इनमें से प्रत्येक पृष्ठ एक गले का भाग होता है। इन गोलों के केन्द्र को, लैंस के वक्रता केन्द्र कहते हैं। इसे प्रायः अक्ष (C) से दर्शाया जाता है। क्योंकि लैंस के दो वक्रता केन्द्र है इसलिए इन्हें, C1 और C2 से दर्शाया जाता हैं।
- मुख्य अक्ष- किसी लैंस के दोनों वक्रता केन्द्रों से गुजरने वाली एक काल्पनिक सीधी रेखा लैंस की मुख्य अक्ष कहलाती है।
- प्रकाशीय केन्द्र- लैंस का केन्द्रीय बिंदु उसका प्रकाशीय केन्द्र कहलाता हैं। लैंस के प्रकाशीय केन्द्र से गुजरनेवाली प्रकाश किरण बिना किसी विचलन के निर्गत होती हैं।
- द्धारक- गोलीय लैंस की वृत्ताकार रूपरेखा का प्रभावी व्यास इसका द्धारक कहलाता है।
- फोकस बिंदु- जब किसी लैंस पर सामांतर किरणे आपतित होती हो तो-
- उत्तल लैंस- इस लैंस में सामांतर प्रकाश की किरणे मुख्य अक्ष के एक बिंदु पर अभिसारित होती है, अपवर्तन के पश्चात्।
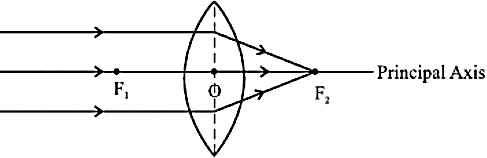
- अवतल लैंस- इस लैंस में सामांतर प्रकाश की किरणे, अपवर्तन के पश्चात् मुख्य अक्ष के एक बिन्दु से अपसरित होती प्रतीत होती है।
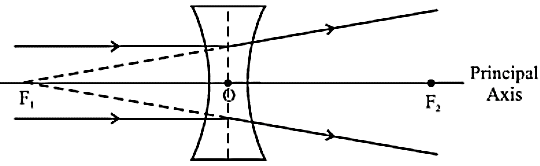
प्रकाशीय केन्द्र O से फोकस बिंदु की दूरी, फोकस दूरी कहलाती है। OF1 = f1; OF2 = f2.
- उत्तल लैंस- इस लैंस में सामांतर प्रकाश की किरणे मुख्य अक्ष के एक बिंदु पर अभिसारित होती है, अपवर्तन के पश्चात्।
- लैंस द्वारा प्रकाश किरण के रेखा चित्र बनाने से पहले
- बिंब से, मुख्य अक्ष, के समांतर आने वाली प्रकाश की किरण अपवर्तन के पश्चात, दूसरी और मुख्य फोकस से गुजरेगी।
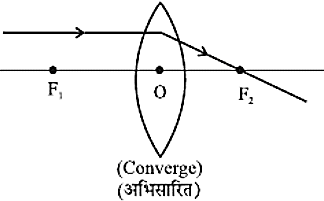
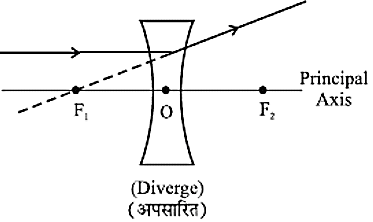
- मुख्य फोकस से गुजरने वाली प्रकाश किरण, उत्तल लैंस से अपवर्तन के पश्चात मुख्य अक्ष के समान निर्गत होगी और अवतल लैंस के मुख्य फोकस पर मिलती प्रतीत होगी।
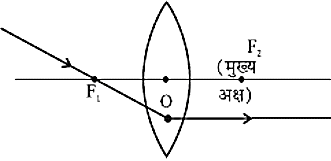
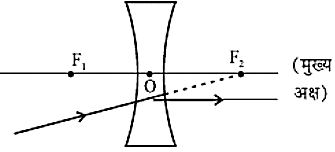
- लैंस के प्रकाशीय केन्द्र से गुजरने वाली प्रकाश की किरण, अपवर्तन के पश्चात बिना किसी विचलन के निर्गत होती है।
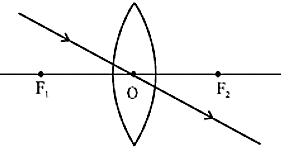
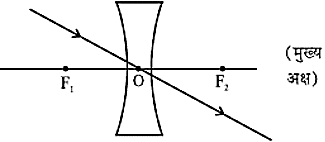
- बिंब से, मुख्य अक्ष, के समांतर आने वाली प्रकाश की किरण अपवर्तन के पश्चात, दूसरी और मुख्य फोकस से गुजरेगी।
- उत्तल लैंस द्वारा प्रतिबिंब बनाना
- बिंब - अनंत पर
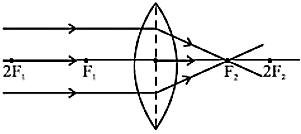
प्रतिबिंब की स्थिति - F2 पर केंद्रित
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब का आकार - अत्यधिक छोटा (बिंदु आकार) - बिंब - 2F1 से परे
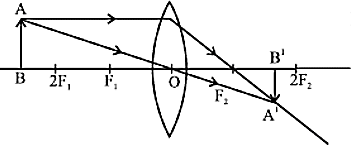
प्रतिबिंब की स्थिति - F2 और 2F2 के बीच
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब का आकार - छोटा - बिंब - 2F1 पर
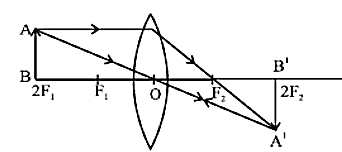
प्रतिबिंब की स्थिति - 2F2 पर
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब का आकार - बिंब के बराबर - बिंब - F1 और 2F1 के बीच
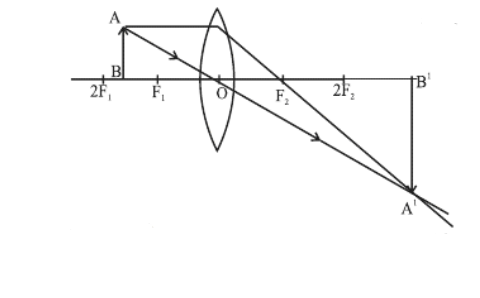
प्रतिबिंब की स्थिति - 2F2 से परे
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब का आकार - अत्यधिक बढ़ा - बिंब - F1 पर केन्द्रित
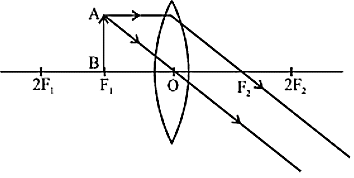
प्रतिबिंब की स्थिति - अनंत पर
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब का आकार - अत्यधिक बढ़ा - विशेष
बिंब - F1 'और प्रकाशीय केंद्र 'O' के बीच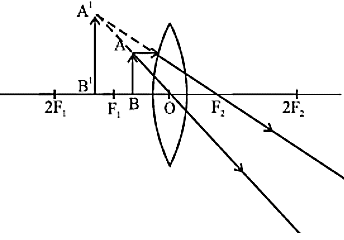
प्रतिबिंब का आकार - अत्यधिक बढ़ा
प्रकृति - वास्तविक तथा उल्टा
प्रतिबिंब की स्थिति - वस्तु के एक ही तरफ
- बिंब - अनंत पर
- Image formation by concave lens
- बिंब - अनंत पर
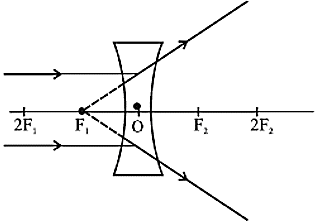
प्रतिबिंब का आकार - बहुत छोटी
प्रकृति - आभासी और सीधी - बिंब - अनंत पर प्रकाशीय केंद्र के बींच (कोई भी बिंदु)
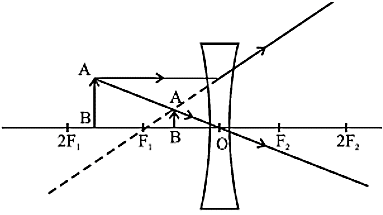
प्रतिबिंब की स्थिति - F1 और O के बीच
प्रकृति - आभासी और सीधी
प्रतिबिंब का आकार - अत्यधिक छोटा
- बिंब - अनंत पर
- गोलीय लैंस की चिन्ह परिपाटी (Sign Convention for Refraction by Spherical Lens)
गोलीय दर्पण की तरह ही गोलीय लैंस की चिन्ह परिपाटी हैं। अंतर इतना है कि लैंस में सभी दूरियां प्रकाशीय केन्द्र से मापी जाती हैं।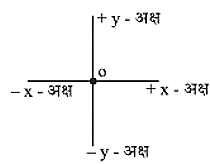
- लैंस सूत्र
'O' प्रकाशीय केंद्र
f फोस और 'O' के बीच दूरी
u बिंब और 'O' के बीच की दूरी
y प्रतिबिंब और 'O' के बीच की दूरी
r वक्रता केन्द्र और 'O' के बीच की दूरी - आवर्धन
आवर्धन को प्रतिबिंब की ऊंचाई तथा बिंब की ऊंचाई के अनुपात के रूप में परिभाषित किया जाता है।
m = प्रतिबिंब की ऊंचाई / बिंब की ऊंचाई = = (1)
h1 - प्रतिबिंब की ऊंचाई मुख्य अक्ष में
h = बिंब की ऊंचाई मुख्य अक्ष से
आवर्धन बिंब दूरी 'u' और प्रतिबिंब दूरी 'v' से भी संबंधित है।
- (2)
अर्थात् (1) and (2)
or
अगर m > | प्रतिबिंब आर्वधित है।
m = 1 प्रतिबिंब, बिंब के आकार के बराबर है।
m < | प्रतिबिंब छोटा हैं। - कुछ छोटी-छोटी बातें जो गोलीय लैंस की चिन्ह परिपाटी को याद रखने योग्य हैं।
बिंब की ऊंचाई (h) हमेशा धनात्मक (+ve)
प्रतिबिंब की ऊंचाई (h1) वास्तविक हमेशा ऋणात्मक (-ve)
आभासी हमेशा धनात्मक (+ve)
बिंब दूरी (प्रकाशीय केन्द्र से) (u) हमेशा ऋणात्मक (-ve)
प्रतिबिंब की दूरी (प्रकाशीय केन्द्र से) (v) वास्तविक धनात्मक (+ve)
आभासी ऋणात्मक (-ve)
फोकस दूरी (प्रकाशीय केंद्र से) (f) उत्तल लैंस हमेशा धनात्मक (+ve)
अवतल लैंस हमेशा ऋणात्मक (-ve) - लैंस की क्षमता
किसी लैंस द्वारा प्रकाश किरणों को अभिसरण या अपसरण करने की मात्रा (degree) को इसकी क्षमता के रूप में व्यक्त किया जाता है।
इसे अक्षर P से निरूपित किया जाता हैं।
लैंस की क्षमता (P) का SI मात्रक ‘डाइऑप्टर' है जिसे (D) से दर्शाया जाता है।अगर f का मान 'मीटर' में है तो
अगर f का मान 'सेंटीमीटर' में है तो
डाईऑप्टर या ID उस लैंस की क्षमता है जिसकी फोकस दूरी एक मीटर हो।
उत्तल लैंस की क्षमता धनात्मक होती हैं।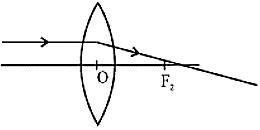
f की दूरी प्रकाशीय केन्द्र से धनात्मक हैं।
अवतल लैंस की क्षमता ऋणात्मक होती हैं।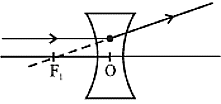
f की दूरी प्रकाशीय केन्द्र से ऋणात्मक हैं।
अनेक प्रकाशीय यंत्रों में अनेक लैंस लगे होते हैं। इस प्रकार संपर्क में रखें लैंसों की कुल क्षमता होगी
